|
| |
|
Слаботочка Книги Если по экспериментальным данным определяются оба параметра распределения Вейбулла, то приближенное решение задачи определения доверительных интервалов для параметров аи b можно получить в предположении нормального распределения оценок. 19.7.4. Доверительный интервал для параметра биномиального распределения. При испытаниях по непараметрической схеме {NUT} мы располагаем только сведениями о числе изделий, подвергнутых испытаниям, и числе изделий, отказавших за время испытаний Т (выборка 2Г). При этом единственным показателем, который может быть оценен, является вероятность отказа q за время испытания. Оценка максимального правдоподобия для вероятности отказа определяется (см. пример 19.1) выражением q = n/N, где п - число отказавших изделий (число условных реализаций выборки); N - число изделий, поставленных на испытания. Известно, что оценка q является случайной величиной, имеющей.биномиальное распределение. Поэтому верхняя и нижняя q доверительные границы для вероятности отказа определяются решениями уравнений: 2 Ci/(l--(/,)-=e; (19.38) ( = 0 2 а<?(1-<?„)-- = е, (19.39) где е - уровни значимости. Численное решение этих уравнений очень громоздко. Компактным и удобным инструментом решения многих задач, связанных с биномиальным распределением, является номограмма, приведенная далее. Номограмма позволяет, в частности, просто и с достаточной для практики точностью определять (7„ и q для любых значений доверительной вероятности у= 1 - е, в том числе и не предусмотренных таблицами. Таблицы и номограмма реализуют функцию вида (19.38). Поэтому уравнение (19.39) обычно преобразуют. Используя известное свойство биномиального рас- N п-1 N пределения 2 = S + S = Ь уравнение (19.39) приводят к виду г = 0 г = 0 i = n S Cn<?UI--?h)- = 1 -е. (19.40) 19.7.5. Определение интервальных оценок с использованием номограмм. Для получения интервальных оценок параметров (показателей надежности) используются таблицы квантилей различных распределений. Для определения квантилей х-распределения, /-распределения, распределений Стьюдента и биномиального можно вместо таблиц воспользоваться номограммами. Методика работы с номограммами демонстрируется далее на конкретных примерах. 1. Номограмма х-распределения. Пример 19.6. В результате испытаний по плану [NRT] при суммарной наработке изделий tx. = 1000 ч зафиксировано п = 5 отказов. Распределение времени безотказной работы изделий экспоненциальное. Определить с доверительной вероятностью у* = 0,8 доверительный интервал для наработки на отказ. Напомним, что если доверительный интервал находится с доверительной вероятностью Y*, то каждая доверительная граница определяется с уровнем значимости е Смирнов С. в., Потапов М. К. Номограмма для функции распределения z-Теория вероятностей и ее применение, 1961, т, VI, вып. 1. = (1 - y*)l2, т. е. в данном случае с коэффициентом доверия у = 0,9 (односторонняя доверительная вероятность). Решение. Верхняя и нижняя границы доверительного интервала для наработки на отказ в этом случае определяются выражениями: где х1, 2п и Xl-8, 2п4-2 -квантили х-распределения по уровням ей 1 - ее чис-цом степеней свободы 2п и 2п + 2. Номограмма х-распределения представлена на рис. 19.5. Левая шкала номограммы - шкала уровней значимости, на которой отмечаются значения е и 1 е. Правая шкала - шкала степеней свободы, на которой откладываются значения 2п + 2 и 2п. Криволинейная шкала в центре номограммы -шкала значений квантилей Х-распределения. Шкала уровней значимости 0,001 -1 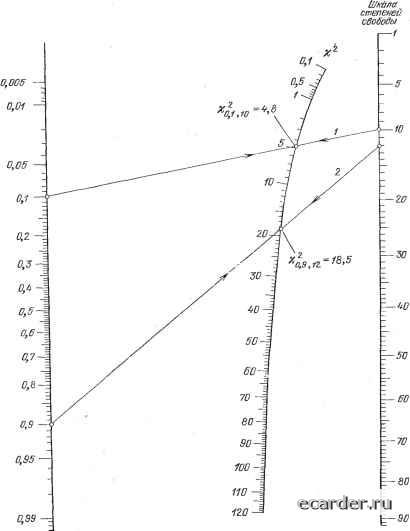 Рис. 19.5. Номограмма -распределения Определение квантилей по номограмме осуществляется следующим образом: между точкой е ==0,1 на левой шкале и точкой 2п = 10 на правой проводится линия 1; между точкой 1 - 8 = 0,9 на левой шкале и точкой 2п + 2 = 12 на правой шкале проводится линия 2; в точке пересечения линии 1 со шкалой % считывается значение Xo.i-. ю = 4,8 (табличное значение 4,87); в точке пересечения линии 2 со шкалой % считывается значение Хо,9; 12 = = 18,5 (табличное значение 18,5). Следовательно, искомые значения границ доверительного интервала для наработки на отказ составляют: Те = 2-1000/4,8 = 417 ч; Гд = 2-1000/18,5 = 108 ч. Распределение % очень широко применяется в различных задачах математической статистики. Во всех случаях квантили распределения практически для любого уровня и числа степеней свободы до 90 могут быть определены по номограмме. 2. Номограмма распределения Стьюдента. Рассмотрим следующий пример. Пример 19.7. На испытаниях некоторого устройства, имеющего время работы до отказа, распределенное по нормальному закону, получено п= 10 полных реализаций (наработок до отказа) х: 120, 110, 80, 130, 120, 140, 80, 150, 130 и 140 ч. Требуется найти с доверительной вероятностью у* = 0,9 доверительные интервалы для наработки на отказ Т и дисперсии D. Решение. Верхняя и нижняя доверительные границы для наработки на отказ в этом случае определяются выражением Тв,и = T±ty,n~i ]/о/(п - 1), где Т и D -точечные оценки для наработки на отказ и дисперсии; tyn-i - квантиль распределения Стьюдента по уровню у при числе степеней свободы п-1. Значения Т и D определяются по экспериментальным данным: Т = - У Xi = l20 ч; D = -i-У (х, -7)2 = 576 ч2. Значение квантили ty,n-i определяется по номограмме распределения Стьюдента (рис. 19.6). Левая криволинейная шкала номограммы - шкала степеней свободы, на которой отмечается значение п - 1. Правая криволинейная шкала номограммы - шкала доверительных уровней, на которой отмечается значение у. Шкала в центре номограммы - шкала значений квантилей распределения Стьюдента. Распределение Стьюдента (/-распределение) относится к классу симметричных, поэтому шкала уровней значимости на номограмме представлена только значениями 1 - ей называется, соответственно, шкалой доверительных уровней. Для опредепения значения квантили между точкой п - 1 - 9 на левой шкале и точкой у = 0,95 на правой проводится линия, в точке пересечения которой со шкалой t номограммы считывается ответ: 4,95; э = 1,87. Следовательно, искомые значения доверительных границ для наработки на отказ составляют Тв,н = 120+ 1,87 ]/576/9-= 120 ч±15ч. Теория вероятностей и ее применение, 1956, т. I, вып. 2. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 [109] 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 |