
 | |
|
Слаботочка Книги 0 1 2 3 4 5 6 7 8 9 10 11 [12] 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199
4.{.5. ВФИ-распределение. В табл. 4.2 приведены нижняя и верхняя оценки для некоторых показателей надежности системы, представляющей собой последовательное соединение элементов, имеющих ВФИ-распределение наработки до отказа, причем предполагается, что известны значения средней наработки до отказа каждого элемента Г. В табл. 4.2 через Г() обозначена k-я из величин Г-, упорядоченных по возрастанию, т. е. Гц) = min Г,; Г(2) = min {Г, Г, >Г,!,},.... протабулированы и приведены в табл. 3.4. Значения е"*** Если дополнительно известны дисперсии af для каждого элемента, то верхняя и нижняя границы вероятности безотказной работы последовательной системы Р (t) могут быть найдены как произведения соответствующих численных верхних и нижних границ вероятностей безотказной работы элементов, приведенных в табл. 3.5 и 3.6. Численные значения границ для наработки до отказа Г в последнем случае могут быть получены численным интегрированием соответствующих границ вероятности безотказной работы. 4.2. НАГРУЖЕННЫЙ РЕЗЕРВ 4.2.1. Предварительные замечания. Предполагается, что отказы элементов обнаруживаются мгновенно после их возникновения и переключения на резерв осуществляется без прерывания работы системы. При этом считается, что переключатель абсолютно надежен, а индикация отказа достоверна. Кроме того, считается, что при переходе на резервный элемент не возникают какие-либо переходные режимы, нарушающие нормальное функционирование. 4.2.2. Резервирование одного основного элемента. Структурная схема резервной группы, состоящей из одного основного и т нагруженных резервных элементов, представлена на рис. 4.2. 1. Вероятность безотказной работы определяется по формуле Р(д==1- П qAto), (4.1) где Qi (to) - вероятность отказа i-ro элемента за время о- Показатели надежности системы из последовательно соединенных «стареющих» элементов Для экспоненциального распределения наработки элементов до отказа, т. е. для Qi (Q = 1 - е"*", при малых справедлива следующая простая оценка снизу: Р(д«1-С+ П (4.2) l<;t<m-l-l где Kf - интенсивность отказов i-ro элемента. При идентичных элементах, что чаще всего бывает на практике, (4.2) принимает вид Р(д«1-(Ч)"+ (4.3) (погрешность данной формулы не превышает б = 0,5 (т + 1) (Яо)"")- Ш2г 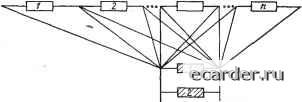 Рис. 4.2. Структурная схема системы из одного основного и т резервных элементов Рнс. 4.3. Структурная схема системы из п основных и т резервных элементов 2. Средняя наработка до отказа в общем случае может быть найдена только численным интегрированием по формуле (4.4) где Р (f) определяется из (4.1). Для идентичных элементов удается записать, компактные формулы: экспоненциальное распределение наработки до отказа каждого элемента р (О = ехр (- U) T = \-k-\ (4.5) при большом т можно пользоваться приближенным выражением f » [С + In (/п + 1) + (2т + 2)-1], (4.6) где С = 0,577... - константа Эйлера; распределение Гнеденко-Вейбулла для наработки до отказа р (t) = = ехр (- Kt) (4.7) Г = Я-«-Г(1+а-1) 2 (-l)*-Q-fi«- или для больших т f In (т + 1)]-; (4.8) идентичные ВФИ-распределения основного и резервных элементов; известно значение квантили г (Т): 0,56/(/п + 1) < г (Г) < \/(т + 1). (4.9) 4.2.3. Скользящее резервирование. Резервная группа состоит из п основных и т резервных элементов, находящихся в нагруженном режиме (рис. 4.3). Выражения для P(t„) и Т приводятся в табл. 4.3, в которой приняты следующие дополнительные обозначения: Р= П PtitoY, (4.10) Pi - сокращенная запись pi (to); Pt - вероятность безотказной работыJ-ro элемента для экспоненциального распределения, т. е. pi = ехр (- ito); 9г = 1 - - Pi> (или 9(i)) - величины Qi (или Qi), упорядоченные в порядке невозрастания, т. е. 9(1) > 9(2) > (или 9(1) > 9(2) >...); yi = U-Pi{to)yPi{to) (4-11) (Yj получается из Yj заменой pj (to) на р (Q); Я(г)-величины Xj, упорядоченные в порядке невозрастания, т. е. К-, > 2) >, Поясним вывод формулы для Р (to) для разных элементов. Резервная группа работоспособна, если в ней имеется не менее т любых работоспособных элементов. Вероятность этого события т-\-п т-\-п п + т т-\-п п + т P(to)= п р1+ 2 п pj+ 2 и Pft+... j = i i=i 7=1 i<t</<:n A=i ... + 2 П 9, П p„ (4.12) где gm - множество ровно tn различных индексов 6 (1, n); gm - дополнительное множество, т. е. g f\ gm = 0, gm \J gm = (1. «); Gm -множество всех g, т. е. всех различных наборов по т индексов из п (число их, естественно, равно Сп+т)- Используя введенные выражения для Р и у, получаем выражение, приведенное в табл. 4.3. Приближенное выражение получается из эквивалентного представления (4.12): / -г- -.-г п+т \ P{to)-l- 2 П 9.- П р+...+ ПЯ1. (4.13) \т+1т+1 ieg+i *eSm+l = 1 / если в нем учесть только первый член в скобках. Приближенное выражение приемлемо при расчетах при выполнении условия max 9г < l/(n + m). (4.14) В табл. 4.3 в нескольких случаях не приводятся точные выражения для Т. Здесь для получения численных значений следует использовать представление Т в виде интеграла от функции Р (4). Точное выражение для Т в случае различных элементов при экспоненциальном распределении можно получить, используя комбинаторную формулу: 0 1 2 3 4 5 6 7 8 9 10 11 [12] 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 |