|
| |
|
Слаботочка Книги Пусть эти корни равны Ь, Ь, .... fcm+i- Это означает, что Bo+BiS + .... + B„»-.iS"+= П [s-bj). 3. Записываем (р (s) условно в виде суммы простых дробей: Ф(8) = -Ь---E + ...+ te , (5.3) rae-~Pj - искомые коэффициенты. 4. Переписываем (р (s) в приведенном виде: (s-bi) (s-b... (s-bjn+i) Раскрывая все произведения и приводя подобные члены, получаем (s-M(s-6,)... (s-6+,) где фг выражены через различные f)] и fc;. 5. Полиномы вида (5.2) и (5.4) равны тогда, и только тогда, когда Л о фо. Л] = ф1, Л2=ф2, Лт = Фт- Из этих уравнений определяются искомые коэффициенты Р;. 6. После нахождения ф; к ф (s) вида (5.3) применим обратное преобразование Лапласа: из выражения определим Примечание. Если ф (s) имеет кратные корни знаменателя, например k равных значений bj, то (5.3) должно быть записано в виде ф(«)=- + - + - + ... + -. S-&1 {s-bjr s-bm+i где k - кратность корня bj. К членам вида P;/(s- bj) применяется соответствующее обратное преобразование Лапласа. 5.1.3. Расчет вероятности безотказной работы. При нахождении вероятности безотказной работы необходимо в графе переходов ввести так называемые поглощающие состояния вместо всех состояний отказа. Это в принципе означает, что следует обратить в нуль все интенсивности переходов из любого состояния отказа. При написании дифференциальных уравнений можно лишь соответствующим образом изменить области суммирования. Для каждого состояния работоспособности k (/г 6 G) можно записать следующее дифференциальное уравнение: где вторая сумма берется по подмножеству тех состояний Е (к), которые одновременно принадлежат Е+. Если граф переходов содержит m различных состояний работоспособности, в результате может быть составлено m различных дифференциальных уравнений. Все эти уравнения и начальные условия вида Pi (0) = pj используются для нахождения вероятности безотказной работы. Для определения искомой характеристики надежности к записанной системе дифференциальных уравнений применяется преобразование Лапласа, в результате чего получается система алгебраических уравнений: 8фь(8) -Pft= -(Pft(s) S Afti+ 2 ih4>i(s)- Решение этой системы уравнений и определение вероятности безотказной работы осуществляются далее так же, как и для нестационарного коэффициента готовности. 5.1.4. Расчет средней наработки и коэффициента готовности. Если ф (s) есть преобразование Лапласа для вероятности безотказной работы, то Т = J P{t)dt= j e-*P(t)dt s = 0 Таким образом, чтобы найти среднюю наработку до отказа (или между отказами), достаточно решить систему уравнений вида -Рй(0)=фЛО) 2 Кг+ S л,,ф,(0) •ее (ft) fe£<fe) для всех /г 6 G. (Эта система получается из (5.4) приравниванием s = 0.) Заметим лишь, что для получения средней наработки до отказа необходимо взять в качестве начальных условий pj (0) = 1 и pj (0) = О для / Ф i, где i - исходное.состояние процесса, а для получения средней наработки между отказами (в стационарном режиме) необходимо взять в качестве начальных условий 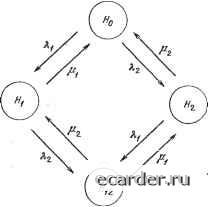 Рг{0)Рг( 2 Pj) Пример 5.1. Рассмотрим восстанавливаемую дублированную систему, состоящую из разнонадежных элементов, интенсивности отказов и восстановления которых соответственно равны: Kl, 7-2, (ij, [i. Граф переходов представлен на рис. 5.1, где Hq - состояние системы, в котором отказавших элементов нет; Hi (Н) - состояние системы, в котором первый (второй) элемент является отказавшим; Нх - состояния системы, в котором оба элемента отказали. Обозначая через р {t) вероятность пребывания системы в состоянии Н получаем две системы дифференциальных уравнений, соответствуюш,их двум случаям. 1. Состояние His. поглощающее: Po{t) = ~(K + K)Po(t) + lPi(t) + \x,if); pl (t) = Кро (О - (2 + M-i) Pi (0; р; (t) = Кро it) - (К + fi2) Р2 (0; Pi., (О = KPi if) + Кр2 (t). Рис. 5.1. Граф переходов для примера 5.1 Р-а Ро (0) о р, (0) Ml М2 о -( + 2) -(> + Mi) 1 о М2 о -(? + М2) Ml -(Ч+Mi) о о [12 -(Я1 + М2) Ml 5.2. «СХЕМА ГИБЕЛИ И РАЗМНОЖЕНИЯ» 5.2.1. Предварительные замечания. Рассматриваются марковские модели восстанавливаемых систем, т. е. таких систем, для которых случайная длительность пребывания в том или ином состоянии, определяемом состояниями ее элементов, имеет экспоненциальное распределение, причем длительность пребывания в каждом состоянии не зависит от предыстории функционирования этой системы. Более того, обычные резервированные системы с восстановлением описываются так называемой «схемой гибели и размножения», которая может быть представлена строго упорядоченной совокупностью состояний. В зависимости от того, сколько элементовв системе может восстанавливаться одновременно, различают два основных режима восстановления: 1) ограниченное восстановление, когда в любой момент времени может восстанавливаться не более одного отказавшего элемента; 2) неограниченное восстановление, когда в любой момент времени может восстанавливаться одновременно любое число от- Ро (О = -{К + К) Ро if) + (iipi (О + V-iPi if)\ pl (О = Кро (О - (2 + fii) Pi (t) + fi2pi2 (0; p2 (0 = 2Po (0 - (1 + 12) p2 (0 + Hipi2 (0; P,it) + pAt) + pAt) + PiAt)=i- Отсюда выражения для средней наработки между отказами Т, до отказа Го коэффициента готовности /С: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 [15] 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 |