|
| |
|
Слаботочка Книги конец, 9о = S <? ()-вероятность отказа системы по одному из монотонных мини-мальных допустимых путей. Обозначим также: я (е) = у Kl (е); К = max X (е); G(X) = minGij(х), T={xdG(x). 27.5.2. Предельные теоремы. 1) lim pf3i > Л==е-. яг-*о I Л!о J Для того чтобы сформулировать результат, в котором дается оценка Мо, наложим на процесс дополнительные ограничения: восстановление отказавшего элемента происходит без пргрывания и начинается либо в момент прихода элемента в ремонтный орган, либо в момент окончания восстановления другого элемента; в предельном переходе число элементов п, функции Gij [х), число обслуживающих приборов ремонтного органа и дисциплина обслуживания фиксированы, а Kl (ё) = К° 8, где Ki (е) фиксированы, а 8 0; мажорирующее распределение G имеет конечный момент т-го порядка. При таких условиях справедливо следующее утверждение: 2) при 8 О К (0) яеп„ а интеграл берется по областиXo>Xi>...>A;m-i; to, ii,..., Im-i- номера последовательно отказывающих для данного пути я элементов; - номер обслуживающего прибора, на который поступает элемент с номером г; / < г. Кроме того, учитывается, что не для всякого из отказашихся элементов найдется доступный для него обслуживающий прибор (элемент с номером to сразу начинает восстанавливаться, а следующий элемент, для которого найдется свободный обслуживающий прибор, будет иметь номер isi). 27.5.3. Частные случаи. 1. Пусть Gi,j (х) = G (х) и каждый обслуживающий прибор доступен для каждого элемента. Тогда в формуле (27.7).. -г-1 (m-r-1)! (Г-1)1 "" 2. Пусть дополнительно Ki (е) = Ki, и если ei = О, то Ki (е) = О, Я = 2 г-Тогда формула (27.7) имеет вид q-JmrI>Kk.-km, . (27.8) где fei< 2 <••< - номера отказавших элементов, т. е. номера единиц в состоянии е» 6-Е-, а сумма берется уже не по путям, а по граничным отказо-вым состояниям е<" для которых т - минимально, 3. Пусть Gij (х) = G {х), все элементы в системе симметричны (случай сколь- зящего резерва), т. е. Я (е) = Яо (ell), где е = S г. и множество переходит в себя при любой перестановке координат ei вектора е. Тогда 9 Jz:i)L уд„ (1) Яо (2)... Яо (/п-1). (и-m)I 4. Пусть Gij (х) == Gi (х). Яг (е) = Я, если = О, Яг (е) = О и каждый элемент начинает ремонтироваться в момент его отказа. Тогда я~ 2К - V. -"гп(*". + -+). где Ть = f c?G,j (О, а сумма берется так же, как и в формуле (27.8). 27.5.4. Двусторонняя оценка вероятности q. Для последнего частного случая предыдущего пункта можно получить двустороннюю оценку вероятности 9 < < <д, где 9 = 2 П(-оь еег t"==l flZft = J x dG„ (x), T;, = j xdG„ (x), a Я (e) = 2Ягг, где сумма берется по всем k, для которых е (k) Е- (другими словами, Я- (е) есть суммарная интенсивность отказа системы в состоянии ё). Глва 28 СПЕЦИАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ СИСТЕМ С ВОССТАНОВЛЕНИЕМ 28.1. СТАЦИОНАРНЫЕ ХАРАКТЕРИСТИКИ ДЛЯ ПОЛУМАРКОВСКОГО ПРОЦЕССА На практике часто возникает необходимость вычисления средней наработки на отказ Т и среднего времени простоя т системы с восстановлением для стационарного процесса функционирования, не описываемого марковским процессом. Пусть рассматриваемая система, состоящая из п восстанавливаемых элементов, может находиться в 2" различных состояниях множества Е, которые могут -быть разделены на два класса: состояния работоспособности (подмножество Е +) и состояния отказа (подмножество £ ). В процессе функционирования система, переходя из одного состояния в другое, блуждает по состояниям внутри одного класса, а затем попадает в другой класс состояний. Переход из подмножества £ + в подмножество £ может осуществляться не из любого состояния работоспособности, а только из граничного (подмножество е+). Аналогично переход из £ в £+ может осуществляться только из состояния,- принадлежащего подмножеству граничных состояний е-. (Примеры подмножества £+, £ , е+, е приведены на рис. 28.1 для условного графа переходов). в случае полумарковского процесса смена индексов (номеров) состояний системы образует марковскую цепь, а время пребьшания в каждом состоянии перед переходом в другое состояние является случайной величиной с произвольным распределением. Предполагаются известными: матрица переходных вероятностей соответствующей марковской цепи Ри Pi2-P2I Pi2- Рт Ргп 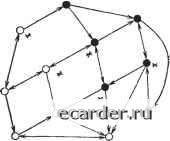 Рис. 28.1. Примеры подмножеств Е- (О) и £+(•) (звез- дочками помечены соответствующие подмножества е+ и е) Рт Рп2 •• Рпп II где Ра вероятность перехода из состояния Hi в состояние Hj] функция Fij (t) распределения длительности пребывания процесса в состоянии Hi при условии перехода в состояние Hj. Можно показать, что в этом случае средняя наработка l& feE. a среднее время простоя r= 2 Pi «ЛИ Pi.Ii Pij) feE Здесь аг = 2 РцТц - среднее время пребывания полумарковского процесса в состоянии Hi. Pi = Di/Dj - стационарная вероятность пребывания марков- 1 = 1 ской цепи с матрицей переходных вероятностей Р в состоянии Hi, где 1-Pi - P12 •• "Plnl -Р21 1 -Pzz •• -Psn ...... -Ро- - Pnl ~PnZ ••• 1-Pnnl Di - минор, получаемый вычеркиванием г-й строки и г-го столбца матрицы D. При марковском процессе задаются интенсивности перехода процесса из состояния Ht в состояние Hj, и формулы для данного случая можно получить как частные случаи для полумарковского процесса. Средняя наработка находится по формулам r=/c(Sp,SXj,)- 7е£ T=K{PiI>K.Jr i& /е£ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 [154] 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 |