
 | |
|
Слаботочка Книги а среднее время простоя по формуле или где Кя k - коэффициенты готовности и простоя: Pi Pk 2 S %t} 2 S , fe£ \fce£ 28.2. СПОСОБ ВВЕДЕНИЯ ФИКТИВНЫХ СОСТОЯНИИ В некоторых случаях предположения об экспоненциальности распределений оказываются неправомерными, причем не удается сделать и предположения о существенной малости времени простоя по отношению к времени безотказной работы. В этом случае может быть использован следующий искусственный прием: вводятся дополнительные фиктивные состояния (фазы), которые позволяют с определенными приближениями описывать немарковские модели. Суть введения фиктивных состояний заключается в том, что распределения с возрастающей интенсивностью отказов (ВФИ-распределения) могут быть получены, если мы просуммируем несколько экспоненциально распределенных случайных величин (т. е. «стареющее» распределение может быть получено как свертка экспоненциальных распределений), а распределения с убывающей интенсивностью отказов (УФИ-распределения) получаются, если произвести «взвешивание» нескольких экспоненциальных распределений. (Вопрос о точности и приемлемости такой аппроксимации должен рассматриваться в каждом конкретном случае особо.) С одной стороны, используя марковскую модель для произвольных распределений, мы упрощаем задачу, с другой:- вводя дополнительные состояния в граф переходов, мы ее усложняем, увеличивая размерность пространства состояний. Простейшие графы переходов для типовых случаев (одиночный элемент, дублированная система), когда распределения наработки на отказ F (t) и времени восстановления G (t) отличаются от экспоненциальных, приведены на рис. 28.2. На рисунке индекс «О» соответствует состоянию работоспособности, а индекс «1» - состоянию отказа. Пример 28.1. Рассмотрим элемент, у которого наработка на отказ имеет экспоненциальное распределение с параметром Яц, а время восстановления - ВФИ-распределение, аппроксимируемое сверткой двух экспоненциальных распределений с параметрами pi и рг» т. е. У. .,. . g (t) = f piPa е- е-У dy. Требуется найти выражение для нестационарного коэффициента готовности. Решение. Система дифференциальных уравнений имеет вид: Pi (О = - КРо (О + 122 (0; Pi{f) = KPoit)~iiPiit); Po(t) + Pi{t)+P2it)= и Ро (0) = 1. 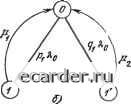 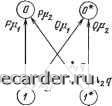 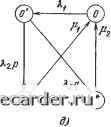 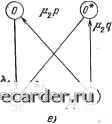 Рис. 28.2, Граф переходов для восстанавливаемого элемента: о) ВФИ-распределение Ж<) и экспоненциальное распределение G(<); б) УФИ-распределение F{ty, е) ВФИ-распределения G(<) и Fd); г) УФИ-распределения F{t) и G«); й) ВФИ-распределение и УФИ-распределение G(t); е) УФИ-распределение F{t) и ВФИ-распределение G(0 Преобразование Лапласа приводит к системе алгебраических уравнений: {К + s) Фо (s) - Р2Ф2 (s) = 1; - оФо (s) + (Pi + s) Ф1 (s) = 0; 5Фо (s) -f s Ф1 (s) + S2 Ф, (s) = 1, откуда после преобразования получаем ф s+(P-i4-a)s4-p-iP-2 Обозначим корни знаменателя Sj, S2, S3: «1,2 = - (а/2) ± V"m; 5з=0, где а = Я,о + pi + Рг; Р = oPi + KVZ + PiP2- Для любых Хо, pi и р2 корни Si и Sgявляются комплексно-сопряженными. Представим фо (s) й виде Фо (S) = Л/s + В /(S - Si) + С/ (S + Sa) = [s (s - Si) (S - Sa)]- [(Л + + В + QS" - (Л (Si + S2) + &2 + CSi) S + Л5152], откуда для определения коэффициентов Л, В и С получаем систему: А + В + С = \; + = - А {Si + Si) - Bsz - Csj-, AsiS = pipg. Окончательно находим: Л = PiP2/(oPi + оРг + P1M-2); В = С = 0,5 (1 - Pipa/P). Отсюда обратное преобразование дает К (О = Ро (О = Pi Р2 /Р + 0,5 (1 - Pip/P) (е-" +  Рис. 28.3. Коэффициент готовности K{t) для примера 28.1: К-ll2/P - стационарный коэффициент готовности; x=л- V Р-0,25а2 Учитывая комплексность и s, окончательно получаем Зависимость нестационарного коэффициента готовности от времени представлена на рис. 28.3. 28.3 ПРОЦЕССЫ МАРКОВСКОГО ВОССТАНОВЛЕНИЯ И АЛГОРИТМЫ ФАЗОВОГО УКРУПНЕНИЯ 28.3.1. Предварительные замечания. В качестве процессов, описывающих функционирование восстанавливаемых систем, как правило, выступают: цепи Маркова, полумарковские процессы с дискретным множеством состояний, многокомпонентные процессы, регенерирующие процессы, процессы с дискретным вмешательством случая. Использование того или иного процесса требует специальных предположений о виде функций распределения наработки элементов и времени их восстановления, дисциплины восстановления и т. д. На практике для расчета показателей надежности чаще всего используются цепи Маркова. Задача оценки надежности сводится при этом к изучению систем линейных алгебраических или дифференциальных уравнений. Возникает вопрос: можно ли указать класс случайных процессов, столь же удобный для описания функционирования восстанавливаемых систем, но не требующий никаких специальных предположений о характере исходных случайных величин? К такому классу относятся процессы марковского восстановления. Идея их построения применительно к восстанавливаемым системам чрезвычайно проста: прежде всего (так же как если бы все исходные случайные величины имели экспоненциальные распределения) кодируются возможные физические состояния системы, затем к полученному таким образом дискретному состоянию системы добавляется непрерывная составляющая (фазовое пространство расширяется) так, чтобы, с одной стороны, компенсировать возможный неэкспоненциальный характер исходных распределений и с другой - обеспечить марковский характер полученных в итоге процессов, которые оказываются процессами марковского восстановления и являются естественными моделями стохастических систем, изменение состояний которых происходит скачкообразно через случайные промежутки времени. 28.3.2. Процесс марковского восстановления. Процессом марковского восстановления (ПМВ) называется однородная двумерная цепь Маркова (х„, е„, п > 0), переходные вероятности которой задаются полумарковским ядром Q it, X, Л) = Р {х„+, е л, Qn+i < tln = х}. Первая компонента (х„, п > 0) определяет состояние системы и образует вложенную цепь Маркова (ВЦМ)в фазовом пространстве состояний {Е, S) с переходными вероятностями р (х. Л) = Q (-f оо, X, А) = Р {х„+1 6 Л !х„ = х). 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 [155] 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 |