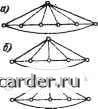
|
| |
|
Слаботочка Книги  Из формул (29.8), (29.10), (29.11) найдем, учитывая разложимость </г>-на-боров при /г > 1: Ro««» = Ф (О,..., 0)-0; Ф«1» pi, г„,, =Ф«0>) 0; i=i t=i ««»=Ri ««» Ф «n>)=i?i «fi» = 21 Pi- Обратим внимание, что в данном случае в качестве показателей <:/г>-набо-ра выбирались вероятности работоспособного состояния элементов, а не отказа, как ранее. Рис. 29.11. Радиальная сеть с п лучами Пример 29.5. Оценивается вероятность связности Ф (</г>) замкнутой однополюсной изотропной сети п-го ранга с радиально-кольцевой структурой. Объекты сети безотказны, вероятность отказа любого канала = q. Решение. Так как структура сети рекуррентна, то можно записать Ф «п» = (1-9-9* + + 29)" + О (п(7) = = 1 -п<7«- rt<7* + nq + 2nq + JlSHziD. qS + o {nq). (29.14) В табл. 29.1 представлены результаты расчета оценок k-то порядка при < 6. В столбце G (<;fe>) изображается только часть исходной сети, содержащая стохастические элементы. Безотказные каналы выделены, причем для простоты изображения стянуты в одну вершину почти все вершины, соединенные каналами, вероятности отказа которых в рассматриваемом <:й>-наборе равны нулю. В столбце h (k) приведено количество одинаковых (в силу рекуррентности и изотропности сети) нетривиальных <:/г>-сетей. При = 5 (вариант б) сеть G (<й>) преобразуется в трехугольную с параметрами отказа каналов q = q, = Ч, Чъ = Ч, при = 6 (вариант б) qi = q, q = q, q = q. Тривиальные <й>-наборы в таблице не представлены. Например, при = 1, 2 все наборы тривиальные, при > 2 - почти все. При = 6 [вариант (в)] <:6>-набор - мультипликативно разложимый и Гбб = Ф (б). В столбце Ф (<;й>) - ft-i/ft даны соответствующие слагаемые для вычисления аддитивной оценки, в столбце r-ii - сомножители для вычисления мультипликативной оценки. В столбцах R, и Rk приведены аддитивная и мультипликативная оценки. Из общего числа 2" различных <;й>-наборов в силу свойства разложимости достаточно рассмотреть всего п (п - 3)/2 -f 7п <:й>-наборов для вычисления аддитивной оценки, и еще меньше - всего 7п <;й>-наборов - для вычисления мультипликативной оценки. Эффективность использования свойства разложимости весьма ощутима. Сравнение оценок в табл. 29.1 с результатом (29.14), полученным по точным формулам, показывает, что точность оценок порядка nq. 29.3.4. Оценка показателей надежности сетей с ординарной структурой. Из предыдущего следует, что разложимые (точнее, тривиальные) <й>-наборы составляют, как правило, подавляющее большинство всех различных <;й>-на- Вычисление оценок k-ro порядка для вероятности связности однополюсной радиально-кольцевой сети
 2n n(n-3) -g5+2g6 + 96 (!-<?«) (1--g*)(l-96) (1-3)2 1-П93 пд4 + +пд5+2пв п(п-3) (1-дз-ga g52g6)" ~ (1 - g3 q.44-g5 j 2g6)n боров при небольших ~ 5 Ч- 10. Однако разложимость устанавливается лишь после построения сети G (<й>) и вычисления Ф (<й>) и Гь-ц. Естественной является задача предварительного отсеивания всех или почти всех разложимых <:й>-наборов, что позволило бы резко сократить трудоемкость оценки. Оказывается, что решение такой задачи возможно для весьма широкого класса сетей, называемых в дальнейшем ординарными. Понятие ординарности излагается применительно к нахождению оценки вероятности связности заданного подмножества объектов сети. По-прежнему предполагается безотказность объектов. (Учет ненадежности объектов ведет лишь к непринципиальным изменениям, но загромождает изложение: например, вместо реберных разрезов графа необходимо рассматривать дополнительно вершинные и вершинно-реберные разрезы и т. п.) Будем называть минимальным <;й>-разрезом множество из k каналов связи, удаление которых нарушает связность сети, причем любое подмножество этого множества таким свойством не обладает. Таким образом, при удалении каналов минимального <:й>-разреза сеть распадается на две подсети с разным в общем случае числом объектов в каждой. Назовем сеть ординарной и имеющей глубину k, если для всех т k при удалении каналов любого минимального т-разреза в меньшей из подсетей, на которые распадается исходная сеть, число объектов не превышает т. Условие ординарности означает отсутствие «узких мест» в структуре сети, что эквивалентно в определенном смысле локальной однородности сети. Установление ординарности сети требует порядка вычислительных операций, что при /г>1ий«5-10 накладывает очень жесткие условия на возможность реализации метода на ЭВМ. Однако для большинства сетей ординарность легко и достаточно достоверно устанавливается экспертным путем на основе визуального анализа изображения структуры. Ниже при описании алгоритма предполагается, что факт ординарности структуры сети установлен заранее. Таким образом, эффективное использование метода предполагает на первоначальном этапе участие разработчика сети. Алгоритм расчета поясняется на примере нахождения мультипликативной оценки вероятности связности всех объектов сети. Предполагается, что объекты безотказны, в противном случае найденный показатель умножается на произведение вероятностей исправного состояния объектов. Основой алгоритма является свойство, что любой неразложимый <:й>-набор может быть представлен в виде объединения минимальных <:т>-разрезов: т k. Поэтому можно вначале выделить <:т>-разрезы и на основе их объединения построить <;й>-набор. Но в силу определения любой <;т>-разрез вырезает «маленькую» подсеть. Последняя может бьггь образована только близко расположенными объектами. Таким образом, формировать <;й>-наборы можно, вначале вырезая «маленькие» подсети, а затем комбинируя параметры каналов связи этих подсетей. Следовательно, при малых k в ординарной сети неразложимые <:й>-наборы образуются только близко расположенными элементами. Понятие расстояния между элементами сети вводится на содержательном уровне, хотя его можно характеризовать, например числом линий связи, входящих в состав минимального пути между соответствующими объектами. На каждом этапе рассматриваются подмножества близко расположенных объектов, каждому из которых ставится в соответствие множество неразложимых <;й>-наборов, образованных показателями надежности примыкающих к этим объектам каналов связи. На начальных этапах близость объектов определяется отношением смежности - два объекта смежные, если они соединяются каналом связи. При возрастании порядка выделяемых <;й>-наборов возможны следующие типы подмножеств объектов: отдельный объект, пара смежных объектов, три попарно-смежных объекта, три объекта, из которых один смежен двум остальным. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 [168] 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 |