
 | |
|
Слаботочка Книги 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 [34] 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 Расчеты для примера 7.9
квадратных скобках записано произведение надежности этого пути на значения Qi, накопленные в четвертой колонке (начиная с первой строки). От члена аЬ, стоящего в первой строке, остается только Ь, так как элемент а входит в состав рассматриваемого пути и поглощается согласно оператору Z. От члена второй строки остается fh, так как элемент g поглощается по той же причине. Вклад третьей строки равен c-b-fh, а четвертой -нулю из-за наличия элемента а, входящего в состав рассматриваемого пути в виде а. Нулевой вклад дают также строки 6, 7. Выражение, стоящее в квадратных скобках, упрощается следующим образом: Ъ Щ - с[к~1ф-ГЩ==Ь{Щ-с~к!с - [Ъс)=Ъс{Н-[ Так же производится расчет всех других путей. Примечание. Аналогичным образом можно воспользоваться перечнем минимальных сечений. 7.6.5. Оценки вероятности безотказной работы для изотропной системы. Назовем систему изотропной, если вероятности безотказной работы всех элементов одинаковы и равны р. Тогда для системы из п элементов prAiff-il -рУ, 1 = 0 (7.15) где Ai - число состояний работоспособности системы при i отказавших элементах. Вычисление р по формуле (7.15) из-за сложности определения всех коэффициентов Ai затруднительно. Раскрытие скобок в (7.15) приводит к знакоперемен- 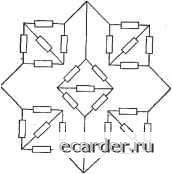 ному ряду, что делает сложным его усечение с целью получения приближенных оценок Р. Более удобные оценки Р основаны на преобразовании т) = (1 - р)/р: i = 0 2 Вт 1 = 0 (Т1+1)« (7.16) Рис. 7.7. Мостиковая схема, допускающая декомпозицию (представление в виде укрупненной схемы, каждый из элементов которой исследуется отдельно) (Т1+1)« где Bi = Сп - Ai - число состояний отказа системы при i отказавших элементах; / - число элементов в кратчайшем минимальном пути системы; с - наименьшее число элементов в минимальном сечении системы; а < п - /; Ь < п. При а = п - I левое, а при b = п правое неравенства (7.16) становятся точными выражениями для Р. Из-за сложности определения коэффициентов Л, и Bj для систем с произвольной структурой их целесообразно использовать для расчета надежности систем с симметричной структурой. Пример 7.11. Определим по формуле (7.16) оценки вероятности Р для системы с той же структурой и характеристиками надежности, что и в примере 7.7. Решение. Ограничимся значением i = 2 как для левого, так и для правого неравенства (7.16). Для этой системы: с = 2; Ло = 1; Л = 5; Л2=8; Вг == 2; т] = » 0,11. В итоге для Р получаем следующие неравенства: (1 + 0,55 -f80,012)71,685 < р < 1 2-0,012/1,685 или 0,977 < Р < 0,985. Обозначим через Hj событие, состоящее в работоспособности всех элементов минимального пути Aj, /= 1, г, системы, а через Rj - событие, состоящее в отказе всех элементов минимального сечения Bj, /= 1, s. Тогда: pPiHj)- 2 P(Я.Я,•J + ...-f Р(Я„, я,д; (7.17) р>РШ,)- 2 Р(Я;,Я/,)+... + S (z. P<1 - 2 P{Rj)-f 2 P{RuRiJ-... ...+ 2 PiRu,...,RiJ, P>l-P{Rj)+ 2 P(hh)-- /=1 1 <il </2< s P(Rj„ RiJ; (7.18) (7.19) (7.20) где P (Hj) и P (Rj) - вероятности событий Hj и Rj, m = 2k -\- 1. Оценки (7.17) и (7.18) являются предпочтительными при малых вероятностях рг безотказной работы элементов системы, а оценки (7.19) и (7.20) - при больших. 7.6.6. Оценки, основанные на декомпозиции структуры. Часто перед тем, как определять или оценивать характеристики надежности системы, бывает целесообразно произвести декомпозицию ее структуры. Рассмотрим пример такого преобразования структуры системы. В системе, изображенной на рис. 7.7, вместо элементов системы рис. 7.2 помещены подсистемы с мостиковой структурой. До расчета вероятности Р безотказной работы системы целесообразно заменить эти подсистемы элементами с вероятностями безотказной работы, равными вероятностям безотказной работы подсистем или их оценкам. Если характеристики надежности подсистем мы заменяем их гарантированньми оценками, то в результате расчета мы также получим гарантированные оценки Р всей системы, но менее точные, чем оценки в примере 7.6, так как исходными данными для расчета будут не точные значения pi, а их оценки. Глава 8 РАСЧЕТ ЭФФЕКТИВНОСТИ ФУНКЦИОНИРОВАНИЯ СИСТЕМ 8.1. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ Наличие определенной функциональной избыточности в структуре большинства сложных систем приводит к тому, что появление отказов отдельных элементов или значительные изменения тех или иных рабочих параметров могут привести не к полному выходу системы из строя, а лишь к некоторому ухудшению качества функционирования и снижению эффективности системы в целом. Для оценки качества функционирования таких систем целесообразно ввести количественный показатель эффективности функционирования, учитывающий влияние таких частичных отказов. Под эффективностью функционирования будем понимать некоторую количественную характеристику качества и объема выполняемой системой работы. Например, эффективность функционирования системы массового обслуживания характеризуется средним числом обслуженных требований (в случае отказов системы и потерь из-за нехватки мест ожидания), средним временем ожидания до окончания обслуживания и т. п. Эффективность функционирования информационных систем может характеризоваться объемом и достоверностью переданной информации. Системы энергетики часто характеризуют дополнительной характеристикой, ущербом потребителя от недоотпуска топлива или электроэнергии. В дальнейшем под эффективностью будем понимать некоторую количественную меру выходного эффекта системы. Если особо не будет оговорено, то предполагается при этом, что чем эффективнее система, тем выше ее показатель эффективности. (Другие случаи, например когда эффективность характеризуется показателями точности и т. п., будут специально разъясняться по тексту). Выбор соответствующего показателя эффективности функционирования в каждом конкретном случае определяется типом системы, ее назначением, видом выполняемой задачи, характером различных внешних условий и другими факторами. Можно оценивать эффективность функционирования систем двух типов: длительного и кратковременного действия. Система длительного действия выполняет некоторую требуемую от нее задачу в течение интервала времени длительностью tf,, начиная с некоторого t. Эффективность функционирования такой системы зависит от конкретной реализации процесса изменения состояний системы в течение этого периода. Система кратковременногодействия выполняет задачи, продолжительность решения которых 4 такова, что за это время система наверняка остается в одном и том же состоянии. Иньми словами, фактически, говоря о системах .чрр.ткоБре-менного действия, подразумевают системы мгновенного действия, т. е.. 10лагаю-, 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 [34] 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 |