
 | |
|
Слаботочка Книги 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 [103] 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 с учетом (7.48) аналитическое выражение переходной функции имеет вид (7.50) Выразим время I и постоянную времени Т в относительных единицах, приняв па базовое значение время в течение которого переходная функция достигает некоторого значения fi(0 = а: t = t*t„; Т = T*i. = t/a„ (7.51) a„=l/n*. (7.52) С учегом (7.51) выражение (7.50) примет МГ) = 1-.-* JmII. (7 Прн / = и Л (г*) = а а принятых относительных единицах время Тогда выражение (7.53) запишется в виде й = 1 - е (7.54) Из (7.54) при принятом m можно найти относительную посгоянную Т*. Аналогично можно найти относительную постоянную Tf, если за базовое время взять 1;. Зная Т* ц Г?", с учетом (7.51) получим для каждого значения m относительные абсциссы t?. = trit, = TtlTr. (7.55) Если объект имеет запаздьгвание Хо, то из (7.55) с учетом обозначений, принятых на рис. 7.5, получаем откуда tiS(T« - "to) = -i - "Со, to = /1й(В,л - тД (7.56) ia = T*/(rf ~ Т„); (7.57) В;, = ТТ/Т*. (7.58) В (7.57) и (7.58) Ag и В;, - постоянные величины для каждого сочетания значений т, а и i. Таким образом, определив значения Тд и т, из экспериментальной переходной характеристики по (7,56) прн принятом т, можно найти время запаздывания То, а затем с учетом (7.51) и постоянную времени Г=Т*(т„-То}. (7.59) При этом аппроксимирующая кривая точно совпадает с переходной характеристикой в точках с координатами (т,, i) и (Т„ й). Таблица 7.8. Значения лпсюянных 7"*, А и S, для а = 0,7 и i = 0,l; 0,2; 0,3; 0,4 в зависимости от степени т аппроксимирующей передаточной функиин
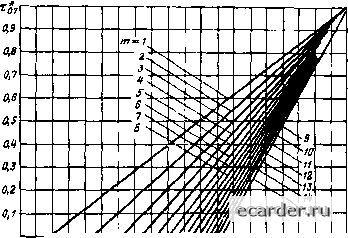 0,1 0,2 0,3 0,4 Q~S 0,S 0,7 0,8 0,3 ffj Рис. 7.6. Графики для определения xJ? = = f(h) Если при расчете величина Tq получается отрицательной, то следует задаться меньшим значением т. Если необходимо обеспечить, чтобы аппроксимирующая кривая совпадала с переходной характеристикой в точках (Tj, () и (т„, а), а также проходила предельно близко от точки то порядок т опре- деляется в процессе расчета. Для это1 о по Т( и Тц определяют значения Тц, соответствующие различным .значениям т. После этого для тех же значений т определ яют То по и Тц. Сравнение полученных значений покажет, что для некоторого значения т величины Тд = f (т, т„) и Tq = f (ту, т„} имеюг наибольшее приближение. Это значение т и следует принять за искомое. При этом величины 7 и Xf, должны выбираться для тех точек экспериментальной переходной характеристики, с которыми точно должна совпадать аппроксимирующая кривая. Для облегчения расчетов в табл. 7.8 приведены значения постоянных 7*, и В;„ для а = 0,7 и (=0,1; 0,2; 0,3; 0,4 в зависимости от степени т аппроксимирующей передаточной функции. Для упрощения записи в индексах при величинах, относящихся к конкретным точкам переходной характеристики, указаны цифры, равные числу после запятой, и соответствующие координаты данной точки, Например, в табл. 7.8 величины А = А. и В,о = В,-7 соответствуют точке с координатами (/ = 0,1; а = 0,7}. Величина Т* = Т? является относительной постоянной времени при базовом значении = tj точки с координатами (а = 0,7; г„) и т. д. Найдем относительное время откуда п. = Ч!а = (г,* + 1,*а)Д1 + Ф- (7.60) На рис. 7.6 и 7.7 представлены графики для Определения относительного транспортного запаздывания x%j=f(x*i-,) и 07 = f{2i) соответственно для различных значений т. Определив из экспериментальной переходной характеристики время тi, при котором ордината 1 = 0,1, или время t2, при котором ордината / = 0,2, я время Х" (при (=0,7), по отношению Xilx-j=x\ из рнс. 7.6 или по отношению хг/х? = т*7 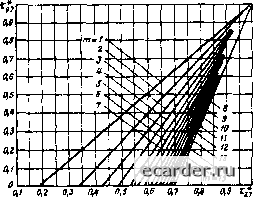 Рис. 7.7. Графики для определения г?? = из рис. 7.7 для нринятого знанення т находят значение величины относительного транспортно! о запаздывания т57=то/т7. По х$7 находят время запаздывания: (7.61) На рнс. 7.S приведена зависимость коэффициента Ов от ординаты й(Гд) аппроксимируемой кривой для различных значений т. Кривые на рис. 7.8 построены по выражению (7.54), н их можно использовать для построения аппроксимирующей кривой при принятом зиаченни Т и найденном значении т, так как с учетом (7.51) н рис. 7.5 ординате h{t„) аппроксимирующей кривой будет соответствовать абсцисса Та = la + Tq = Ttta -t- Tq. (7.62) Из (7.62) также следует, что с помшцью графиков на рис. 7.8 можно иайти постоянную времени - Т = (т„-То)/а„ (7.63) определив, например, tq с помощью графиков на рис. 7.6 или 7.7. При наличии запаздывания то в объекте и коэффициенте его передачи, равном ка, определив значение постоянной времени Т, с учетом (7.48) получим передаточную функцию объекта в виде И«б(р) = (7-64) (Гр + 1)" Если вршя транспортного запаздывания известно, то 5-о6раэную переходную характеристику объекта можно аппроксимировать кривой, динамические свойства которой определяются передаточной функцией (7.49). 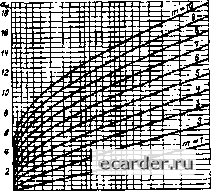 Рис. 7.8. Зависимость коэффициента от ординаты h (tJ аппроксимируемой кривой Передаточные функции этого вида позволяют аппроксимировать S-образные переходные характеристики таким образом, что аппроксимирующая кривая совпадает с экспериментальной кривой в точках с координатами (то, 0), (ti. О, (1„, а) (см. рис 7.5). При этом кратность передаточной функции я может быть задана произвольно. Если требуется иайти такую кривую, которая будет совпадать с экспериментальной в указанных точках и, кроме того, должна проходить предельно близко от третьей промежуточной точки (т;,Д то число и определяется в процессе расчета. Аппроксимация передаточными функциями вида (7.49) при кратности и = 1 -г 10 может быть выполнена по графикам, приведенным на рис. 7.9 и 7.10, на которых даны зависимости TX = Tilt-, и T\ = Tiltn от tXi = tilt-i (рис. 7.9) или от tTtfti (рис. 7.10). Для определения Tj и Гг при принятом п необходимо располагать координатами двух промежуточных точек экспериментальной переходной характеристики (1,; 1=0,1) [или (Гг; 1 = 0,2)] и ((т;/ = 0,7), в которых аппроксимирующая кривая должна точно совпадать с экспериментальной. После нахождения по графикам на рис. 7.9 (или на рнс. 7.10) значений Т\ к Т\ определяют дствительные значения постоянных времени: Г, = Ttr,; Tj = Г!(,. (7.65) Если аппроксимирующая кривая должна пройти через две промежуточные точки и располагаться на предельно близком расстоянии от третьей промежуточной точки, то расчет следует производить с использованием графиков Т*1 = f{t*n); Tf (tXj) (рнс. 7.9) и Tt=/(rS,); Г5 =/((!,) (рис. 7.10). Графики, приведенные на рис. 7.9 и 7.10, позволяют определить я, 7 и Т при условии, что аппроксимирующая кривая совпадает с экспериментальной в двух точках с ординатами Л (О = 0,2 и hU) = 0,7 [или Л(0 = 0,1 и й([) = 0.7] и будет проходить на предельно близком расстоянии от точки с ординатой Л(г) = 0,1 [или Л(г)=0,2]. Определение ТХ и Т? производят в этом случае для я tJ, по обоим рисункам для нескольких значений п. Окончательно выбирается то значение п. для которого Tf и Т имеют наибольшее совпадение. За искомые принимают постоянные времени 7 и 71, соответствующие точкам, через которые точно должна пройти аппроксимирующая кривая. Если объект имеет коэффициент передачи коб и время транспортного запаздывания 1о, то после определения постоянных вре- 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 [103] 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 |