
 | |
|
Слаботочка Книги 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 [104] 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 Подробности химчистка здесь. 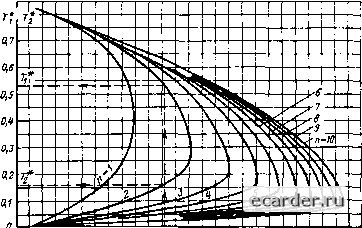 0,т 0,20 0,24 0,28 0,32 0,3S tjy0,40 0,44 0,48 0,52 0,50 0,00 0,041, Рис. 7.9. Графики для определения относительных постоянных времени в передаточной функции (7.49} по относительному времени г?7 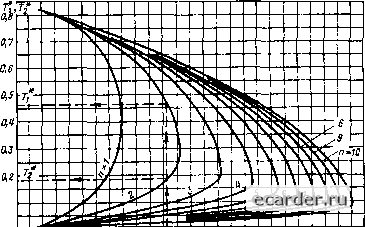 0,1 О 0,03 0,10 0,14 0,18 0,22 0,2В tfj0,30 0,34 0,36 0,42 0,46 0,50 0,54 tj Рис. 7.10, Графики для определения относительных постоянных времени в передаточной функции (7.49) по относительному времени мени получаем передаточную функцию объекта в виде Иоб(р) = (7.66) ХТ,р+\){Т2р + Ц" Рассмотрим несколько примеров определения динамических характеристик обьектов регулирования по изложенной методике. Пример 7.2. Определить передаточную функцию нагревательной печи по ее S-образной переходной характеристике, полученной экспериментально при возмущении со стороны регулирующего органа (РО) путем его быстрого открытия xobj; = 8 % полного хода. До возмущения температура в печи была ©о = 134 °С. Установившееся значение температуры после окончания переходно! о процесса ©уст = 152 "С. Так как значение транспортного запаздывания заранее неизвестно, то будем искать передаточную функцию объекта в виде (7,64) при совпадении аппроксимирующей характеристики с пере- ходной характеристикой объекта в точках (тг, 12} и (Т7, (7). Из переходной характеристики /i(f) (характеристика ие приводится} найдено, что при i = 0,2 = /1(12) время Ti= 15 с, а прн ( = 0,7 = Л(т7) Время т7 = 23 с. Решение: 1) определяем коэффициент передачи объекта (152 - 134) Таблица 7.9. Значения х переходной функции объекта из примера 7.3 при различных значениях т Лоб (0ус1 - ®o)/Xq„ = = 2,25 град/% хода РО; 2) задаемся значением m = 3, 3} по табл. 7.8 zuifl m = 3 находим Т = 0,277, Л27 = 0,738 и В27 = 2,355; 4} по (7.56) находим транспортное запаздывание То = 27(52712 - "l) =0,738 X X (2,355-15 - 23) = 9,1 с; 5) по (7.59) находим постоянную времени 7= Т(Т7 - То) = 0,277(23-9,1) = 3,85 с. 6) искомая передаточная функция нагревательной печи Б соответствнн с (7.64) имеет вид 2-25е"* »об(р) = -~у град ода РО. Прнм 73. Определить передаточную функцию объекта по переходной характеристике нз примера 7.2 с = 13 с, Хз = 15 с и т7 = 23 с при условии, что аппроксимирующая кривая должна пройти через точки с координитамн (15 с; 0,2) и (23 с; 0,7) и находится на предельно близком расстоянии от точки (13 с; 0,1). Решение. По (7.56) и табл. 7.8 д.м нескольких значений т определяем to = = /(ti; t,) и То = /(21 "7) и находим их разность. Для m = 6 находим Ч = f{i,т) = An{Bnl -Х7) = = 0,818(2,223-13 - 23) = 4,825 с; Ч = /(-2 ; т) = 27 (B27ti - t,) = = 1,257(1,795-15 - 23) = 4,934 с. Аналогично определяя to для m = 7, 8 и 9, по полученным результатам составляем табл. 7.9. Минимальное по абсолютному значению Дто имеет место при m = 7. Следовательно, искомыми m и То в соответствии с условием задачи будут m = 7, to = 3,797 а 3,8 с. По (7.59) и табл. 7.8 для m = 7 находим Т = 7l(t, - to) - 0,123(23 - 3,797) = = 2,362 » 2,36 с.
Таблица 7.10. Значешя т57 переходной функции объекта из примера 7.4 при различных значениях т
Искомая передаточная функция имеет вид Жоб(р)=2,25е-з-7(2,36р-1-1) град/% хода РО. Прнмер 7.4. Решить пример 7.3 с помощью графиков, представленных на рис. 7.8-7.10. Решение; 1) находим относительные временные координаты: -с*, =ti,/t7 = 13/23 = 0,565; t?7 = tj/t, = 15/23 = 0,652: 2) по т7 и t57 для различных значений m = 6, 7, 8 и 9 находим по графикам на рис. 7.9 и 7.10 значения относительного транспортного запаздывания. Результаты сводим в табл. 7.10; 3) по наименьшему абсолютному значению разности tS7 = /(т7) и tg, = /(х57) принимаем m = 7; 4) по (7.61) определяем время транспортного запаздывания: Хо = t57t7 = 0,165-23 = 3,8 с; 5) по графику иа рис. 7.8 прн базовом значении А (г) = 0,7 и m = 7 находим значение Ota = 8,13; 6) по (7.63) находим постоянную времени: Т = (т, - то)/а„ = (23 - 3.8)/8,13 = 2,36 с; 7} находим переда I очную функцию объекта: об(р) = 2,25й "7(2,36/)+ 1}. Пример 7S. Определить передаточную функцию объекта в виде (7.66) по его экспериментальной переходной характеристике, для которой То = 0; = 25 с и f7 = 67 с. Аппроксимацию требуется вьшол-нить прн п = 2. Коэффициент передачи объекта Лоб = Решение: 1) находим относительное время: i5, = ГгАт = 25/67 = 0.373; 2) по [рафику на рис. 7.10 при и = 2 находим относительные значении постоянных времени: П = 0.565 и Т5» 0,141; 3} по (7.65) находим Г, = = 0,565-67 = 37,9 с; Т1 = 0,141-67 = 9,47 с; 4) находим передаточную функцию; ф(Р) = УШ9р + 1)(9,47р + 1)]. Пример 1.6. Определить передаточную функцию объекта в виде (7.64) по его эксперимевта;1Ьиой переходной характеристике при условии, что аппроксимирующая кривая должна пройти точно через точки с координатами (45 с; 0,2) и (110 с; 0,7) и близко от точки (33 с; 0,1) при to=0. Решение: 1) определяем значения = ii/l, =33/110 = 0,30; Г, = ГзД, =45/110 = 0,41; 2) по графикам на рис. 7 9 и 7.10 для нескольких п находим 7 ? и 7 как функцию г7 и г57. По результатам составляем табл. 7.11; 3) из табл. 7,11 видно, - что наиболее близкое совпадение постоянных времени ТХ и Т% имеет место при «= 3. Поэтому в соо1ветствии с условием задачи окончательными будем считать и = 3, = 0,538, 75 = 0,107; 4) по (7.65) определяем посюянные вре-мстш Ti и Tj: Г, = Tt = 0,583 110 = 59,2 с; rj = 711, = 0,107-НО = 11,8 с; 5) находим искомую передаточную функцию: Иоб(р) = 1/[(59.2р -Ь 1)(11.8р -Ц 1)]. Определение частотных характеристик. Проведение экспериментов по определению КЧХ с помощью периодических воздействий связано с большими 1ехническими трудностями, так как продолжительность опыта на одной и той же частоте со в среднем в 5-10 раз больше времени установления переходной функции h(t), В связи с этим необходимо более тщательно стабилизировать источники возмущений, а также контролировать смещение средней линии выходных колебаний. Эксперимент заключается в том, что испытательное периодическое воздействие с заданным периодом Гпер подают на вход объекта до тех пор, пока на его выходе не установятся кааебания выходной в&пнчины у(г) с частотой (а = In/Tefr Признакоти установившихся колебаний выходной величины y(t) является идентичность колебаний по амплитуде на трех -пяти периодах; при этом общая продолжительность опыта равна (6- 15)Т,ер. Эксперимент следует начинать с определения переходной характеристики объекта для получения КЧХ на нулевой частоте (ю = 0). Затем иа вход объекта подают колебания с часютой io„, прн которой сдвиг фаз между входными и выходными колебаниями составляет 180°. Для нахождения (й„ достаточно объект ввести в режим двухпозиционного регулирования с зоной нечувствительности, близкой к нулю. Двухпо- Таблица 7.11. Звачения 7 и 7 переходной функции объекта вз пртмера 7.6 при риишчных зцячешшх п
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 [104] 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||