Слаботочка Книги

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 [105] 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

зиционное регулирование является верхним пределом диапазона рабочих частот для систем с ПИ-регулятором. Далее следует снять частотную характеристику в диапазоне рабочих частот процесса регулирования, например при частотах, равных 0,8; 0,6; 0,4 частоты двухпознционного регулирования. При проведении эксперимента целесообразно записывать колебания входной и выхошюи величин иа одной диаграммной бумаге.

Важным фактором прн планировании эксперимента является выбор испытательного периодического воздействия x{t). Желательным видом входных воздействий являются синусоидальные колебания, В линейной системе колебания на выходе объекта могут отличаться от колебаний на входе только по амплитуде и фазе. Чтобы получить КЧХ объекта прн синусоидальных колебаниях, достаточно обработать выходные и входные колебания для ряда различных частот ш. В общем случае применение синусоидальных воздействий x{t) =Asinmt упрощает последующую обработку результатов эксперимента, однако для создания таких cniHajioB необходим специальный генератор катебаиий.

Испытательные сигналы типа .4„x<;inu)f при экспериментальпом определении КЧХ удобно применять на объекте, на котором смонтирована АСР выходной величины y{t), имеющая в законе регулиротания интегральную составляющую. При этом структурная схема снятия частотнмх характеристик объос-та с использованием автсшатнческого регупятора самой снстемы имеет вид, представленный на рис. 7.П. При проведении эксперимента регулятор опытным путем настраивают таким образом, чтобы переходные процессы в системе затухали достаточно быстро. Затем на задатчик регулятора подают синусоидальный сигнал и регистрируют установившиеся колебания x(t) н y(f).

Система регулирования будет следящей

yftj

Рис. 7.И. Структурная схема снятия КЧХ объекта с использованием автоматического регулятора:

1 - объект; 2 - генератор колебаний; 3 - регулятор; 4 - регистрирующий прибор; 5 - регулируго-ший орган

относительно сигнала генератора колебаний. При этом, если частота среза КЧХ объекта лежит в области рабочих частот регулятора, вынужденные колебания выходной величины у (г) [а при низких частотах и входного сигнала л (г)] будут гармоническими даже при наличии нелииейностей в РО. Достоинствами такой схемы являются отсутствие дрейфа оси колебаний выходной величинм и обеспечение сохранения хода технологического режима, так как в процессе проведения опытов автоматически поддерживается в среднем нормальный режим работы объекта. Для упрощения опытов удобно возбуждать на входе в объект периодические колебания в виде прямоугольной (для мембранных ИМ) тлли трапецеидальной (при использовании ИМ с постоянной скоростью) волн.

Метод прямоугольной волны не требует применения генератора колебаний и линеаризации расходной характеристики РО. Периодические колебания в внде прямоугольной волны могут создаваться вручную любым РО, имеющимся на входе исследуемого объекта. Однако при использовании этого метода прн обработке результатов опытов приходится разлшать в ряд Фурье колебания входных и выходных величин.

При снятии КЧХ методом прямоугольной волны возможны два способа:

1) на вход объекта подают прямоугольные периодические колебания с постоянным периодом. После двух-трех колебаний на выходе измеряют амплитуду колебаний и их сдвиг по фазе относительно входных колебаний. После этого изменяют период входных колебаний, ие меняя амплитуды, и снова после двух-трех колебаний измеряют амплитуду и фазу выходных колебаний. Опыт повторяется на каждой точке КЧХ. Существенным недостатком этого способа является дрейф средней линии колебаний, особенно при наличии в объекте интегрн-руюших элементов или нестабилнзированных источников помех;

2) на вход объекта подают постоянное воздействие х (I) = -t- А н при отклонении выходной величины иа y(t) = +М скачком изменяют входное воздействие до значения x{t) = - А. При уменьшении выходной величины до значения у(0 = -М снова скачком устанавливают значение входной величины X (Г) = + А. В дальнейшем опыт повторяют (рис. 7.12). Так как по этому принципу работают двухпозиционные регуляторы при зоне нечувствительности, равной 2М, то этот способ снятия частотных характеристик часто называют методом двухпозиционного регулирования.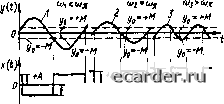

Рис. 7.12. Определение КЧХ объекта методом прямоугольной волны

y(t) о

Рис 7.13. Обработка входных и выходных колебаний

Следует иметь в виду, что при снятии частотных характеристик методом двухпозиционного pei улирования вследствие инерционности объекта регулирования после изменения знака возмущающе! о воздейсз вия выходная величина продолжает некоторое Время изменяться в прежнем направлении и выходит из заданной зоны +М. Поэтому заданная зона должна обеспечивать колебания не более допустимых отклонений параметра по технологическому режиму.

Если зона изменения ус = 2М = 0 и входное воздействие x(t) = ±А будет изменять свой знак при проходе y(t) через нуль, то выходная величина y{t) будет гармонически колебаться (кривая 2 на рис. 7.12} с частотой <и„.

Если изменение знака входного воздействия будет Производиться на границах зоны у (I) = = -I- М. го выходная величина будет совертпать гармонические колебания с частотой (О 7

При этом, если изменение знака входного воздействия производить при входе выходных колебаний в зону уо = ±М, частота колебаний у (г} будет больше (й„ (кривая 1 на рнс. 7.12), а если изменение знака x(t) производить при выходе у([) из зоны Уо=+М, частота колебаний y{t) будет меньше О), (кривая 3 на рис. 7.12). Степень уменьшения и увеличения колебаний y{t) возрастает при увеличении зоны уо = ±М. Таким образом, при каждом фиксировацном значении Уо, методом двухпозиционного

регулирования можно снять значения частотных характеристик в двух точках при гиц < oj„ и 0)э, > oi„. РГшененяем амплитуды возмущающе! о воздействия или ширины зоны Vq можно noJjy4HTb качебання выходной величины требуемой частоты.

Обработка записей входных и выходных гармонических колебаний начинается с выбора нескольких периодов установившихся колебаний и проведения средних линий х = 0 и у-О (рис. 7.13). Значения 4((й,) определяют как отношение максимальных амплитуд входных Ах, и выходных Ду, колебаний для данной частоты ш,:

Л (01,) = Ayj/Ax,.

Для нахождения фазового сдвига определяют отрезок времени АТ„ между моментами пересечения x{t) и у (t) средних значений х ~0 и j; = 0 в одном н том же направлении; значение фазочастотной характеристики на данной частоте ф(сВ() = = Д7„ер/7"пер-360°. После определения А(о}) и ф{о)) на всех частотах ш, строят КЧХ. При разбросе отдельных значений КЧХ ее сглаживают Для этого на практике прибегают к выравниванию точек КЧХ от руки или осуществляют сглаживание частотных характеристик каким-либо аналитическим выражением, например с помощью метода наименьших квадратов.

Если испытательный сигнал имел форму прямоугольной волны или входные и выходные колебания были искажены помехами, то обработка результатов эксперимента осуществляется разложением функций x(i) н у (г) в ряд Фурье. При хорошей фильтрации высших lapMOHHK, что имеет место для 1?ольшинстяа промышленных объектов, прн расчете можно ограничиться первыми гармониками входных и выходных колебаний.

Рис. 7.14, Обработка результатов определения КЧХ методом 12 ординат

Первые гармоники из колебаний, искаженных помехами, удобно выделять по методу 12 ординат, который заключается в следующем (рис. 7.14}. Период анализируемого колебания разбивают на 11 равных частей и от произвольного уровня измеряют ординаты

у(г,) = y{iX 1=0, 1, 2.....11. Разложение

функпни в ряд Фурье имеет вид

у (£} ад До + fll COS (27t/Tnep) t + + г»18]П(27г/Гпер}г.

(7.67}

Коэффициенты разложения с учетом (1.54} и (1.55} находят из следующих выражений:

уф; fli =4{у(11)-у(5} + о

+ 0.5[>(l} + .V(9}-y(3)-y(7}] + + 0,886 [>(0} + у(10}-у(4)-у(6}]};

bi = у {у(2) - у(8) -Н 0,5 [у (0) + у(4) -

- у (6} - у (10}] + 0,866 [у (1} -Ь y(3)--.V(7}- у(9}]}.

Коэффициент flo определяет среднюю линию, относительно которой совершаются гармонические колебания.

Коэффициенты а, и bj определяют амплитуду колебаний относительно средней линии. Обозначив эти коэффициенты для функции у{[) для различных частот Uiy и biy, а для функции х ([) - соответственно Щх и bix, находят значение АЧХ на частоте ш,-:

((й,} = 1/(4 + ь1}/(а, + й,).

Определение динамических характеристик объектов регулирования статисгическим методом. В основе статистических методов определения динамических характеристик объектов регулирования лежит интегральное уравнение

Ry, (т) = f К, (т - ?.) w (к) dX + R„, [z), (7.68}

позволяющее по корреляционной функции К{х) сигнала x{t) на входе обьекта

Рис. 7.15. Модель объекта регулирования 320

(рис. 7.15) н взаимной корреляционной функции (т) между выходом у (I) и входом л(() найти импульсную переходную функцию w{t). Обычно принимается, что входное воздействие и помеха n(l} не зависят друг оз друга н их взаимная корреляционная функция R„{x) = i). В этом случае выражение (7.68) принимает вид

7?,,(т)= ] К,{Х-Х){Х]<1Х. (7.69)

Основным преимуществом статистических методов по сравнению с обычными методами определения динамических характеристик путем подачи принудительных сигналов x{t) является небольшое влияние помех на результаты расчетов. Решение уравнения (7.69) может быть найдено как во временнбй, так и в частотной области.

Решение во временнбй области основано на замене интеграла (7.69) конечной суммой, для чего интегральное уравнение (7.69) заменяется конечной суммой на участке реализации Т:

(7.70)

Полагая т = О, ДА., 2 ДХ,...,(« - 1) ДА., получаем п уравнений с п неизвестными, которые позволяют определить значения w{X) в точках

А. = 0;

« - 1 п - 1

;...;Т.

Матрица системы при этом имеет вид

КтЛЩ Кг,{Щ...Кг,\{п-\)АХ-\

КтЛЩ K7v,(0)... КтЛ(н- 1)Щ

Кт.[(«- 1)Д?ь] Кт\{п-1)М-]...КгМ

(7.71)

Недостатком решения во временной области является то, что незначительные погрешности в определении корреляционной и взаимной корреляционной функций приводят к существенным погрешностям в определении импульсной переходной функции.

Решение в частотной области основано на преобразовании Фурье уравнения (7.69) и переходе к спектральным плотностям, в результате чего получаем

5Лсо) = Ж(/а))5Л<й).

(7.72)

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 [105] 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121