
 | |
|
Слаботочка Книги 0 1 2 3 4 5 6 7 8 9 10 [11] 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 https://www.eduvet.ru онлайн обучение кардиология. 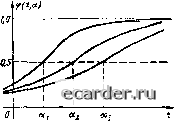 Рис. 1.12, График функции ф (Г) = 1/2 + + (I/jr)arctg[(r - а)/я*] при а, < Яг < otj Дельга-функция математически опреде-ляегся соотношением b(t)=hm= lim а- о д! а Ол lit - а) + а*1 О при /ф О; сс при t = 0. (1.233) Физически дельта-функция представляет собой илшульс бесконечно большой ллгпли-туды и бесконечно малой д:ш(е)[ьнос1и, нричш ,дпя нее имее! сипу соотношение j b{t)dt= 1. (1.234) Производная /-Г0 порядка от дельга-фуикции определяется соотношением [S(r)]=hm>*"» (1.235) Пример 1,21. Рассмотрим авт омати-ческую систему регулирования, описываемую дифференциальным уравнением вида у(0=Л Определим реакцию системы на единичное воздействие при нулевых начальных условиях, т. с. найдем решение уравнения у It) при ] при.>0; ( О цри f < 0. Преобразовав дифференциальное уравнение по Лапласу при нулевых начальных условиях, получим У(р) = ЧТср + т,р + ш откуда y[t)kiTlb{t)-TMt)+ 1]. 9. Начальное и предельное значения оригинала. Если функции ф(г) и ф(() являются ори1иналами, а ф (р) - изображение ориги- нала ф(£). то при существовании предела iimtp(t) справедливы равенства (1.236) hm рф(р) = )1тф(1); р-. ос 1 - 0 1ш1рф(р)= 11тф(г). (U37) Дискретные функции При исследовании автоматических систем регулирования приходится иметь дело с дискретной последова1еяьностью прямоугольных импульсов различной амплитуды н длительности. Ош1саиие процессов в таких системах производится с помошью специальных лщскретных функций: решетчатых и смещенных решетчатых (рис. 1.13). Решетчатой называется такая функция, значения которой определены лишь в дискретные, равноотстоящие момен гы вршени, В отличие от непрерывной функции х[1) решетчатая функция обозначается х[иТ], и по определению х[пГ] = x(t) при ( = пГ, (1,238) где Т - интервал дискретизации по времени; и - любое целое число. Смешешгая решетчатая функция обозначается X [нТ, At], и по определению х[п7, Дг] = х(0 при t = «Г + Дг, (1,239) [.че-О < Д( < Г. Одной и той же функции x{t) соответствует одна-сдинс1 венная решетчатая функция х[пТ], обратное же утверждение будет неверным. Одной и юй же решетчатой функции могут соответствовать различ- 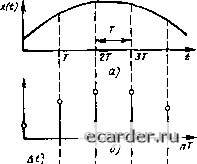
Рис. 1.13, Непрерывная функция (я) и соответствующие ей решетчатая (б) и смещенная решетчатая (в) функции Рис 114. Решетчатая функция и ее о1ибаю-щие п п*1 п Рис. 1 15. Первая разность решетчатой функции ные непрерывные (н лаже разрывные) функции, если только их ординаты в дискретные моменты времени г = нТ равны ординатам (дискретам) решетчатой функции. Эти функции называются огибающими реше! ча-той функции (ш1риховые линии на рис 1.14). Исследовать решетчатые функции удобнее в относительном масштабе времени 7 = t/T; е = А(/Т, (1.240) тогда x[nj=x(f) при t = n: (1.241) х\п, ej = x(fi) при ti = п - с. (1.242) Скорость изменения ренгетчатои функции характеризуегся ее первой ра1НОСтью (рис 1.15), или разностью первого порядка Дл [и] = [п + 1] - (1.243) Разность в юрою порядка Дх [п] = Лх [п ч-1} - Ах [п] = = x[n-t-2] -2x[«-t- 1} -t- \[«]- (1-244) Разность к-го порядка АЧ[«] = Д-х[л-»1]-А-ЧИ = Во мнотих случаях поведение дискрС!-ных автома1ических систем можно описать линейными pajHOCTHbiMH уравнениями с постоянными коэффициентами в форме + b.-iA V[«} + . + bf,y\fi] = X[п]. (1.246) Здесь правая часть уравнения является известной заданной функцией x[nj, а уп} - иск<1мои функцией, представляющей собой решение разностного уравнения. Если в (1.246) заменить раиюсти решетчатой функции у[и] их )начсниями по (1 245), то получится иная форма записи разностного уравнения. %у[" + iv[n-t-fc- 1] + ... + аоу[п] = - х[п]. (1.247) Коэффициенты а а h связаны следующими соотношениями: i bi.,= )a,i , (1,249) Li (;-v)(*-/)! Решение разностных уравнений вида (1.246) и (1.247) значительно упр01цается, если воспользоваться дискрет ным преобразованием Лапласа. Основные этапы решения сводятся к следующим. 1) функции у[п] и х[п] всшествеиноВ переменной п преобразуются в функции yiq) и х{д) комплексной переменной g = а + /Й, называемой параметром преобразования; 2) находится решение для функции y{q); 3) найденное решение для y{q) преобра-*уегся в у[п]. Дискретное преобразование Лапласа для решетчатых функций определяется соотношением х(?)= X К п = 0 (1.250) Для Смещенных решетчатых функций л(«)- Z б~"х[(1, fJ (1,251) Так как параметр е не влияет иа свойства дискре1но10 iipeofipa 1ования Лапласа, го в дальнейшем рассмафнвается лишь функция х[п] Если .для функции х[п] можно указа! ь такие не 1ависнтцие or и постоянные а и Ь, что при любому > о выполняется неравенство \х[п]\< ае", (1.252) то ряд (1.250) сходится при всех < Ь, где Ос - абсцисса сходимости. Помимо одностороннего дискретного преобразования Лапласа (1.250) вводится двустороннее дискретное преобразование Лапласа (1.253) Если при fl < О х[«]=0, то двустороннее дискретное преобразование Лапласа сводится к Одностороннему, которое и рассматривается в датьнейшем, если нет специальных оговорок. Если н (1.250) положить г Л (1.254) x(z)- t (1-255) называется z-преобразованием. Прнмер 1.22, Пусть хМ= IW, тогда Рассмотрим основные свойства дискретного преобразования Лапласа. Для сокра-П1ения вместо (1.250) будем использовать символическую запись x(g) = D{xH); (1.256) x[n] = D-{xiq)}. (1.257) 1. Линейноегь преобразования. Если x,{q) = D{xt[n]}; . I ciiXiiq) = 0 2] а,х,[п]}, где Hj - постоянные величины. Аналогично если (1.258) x,[n-] = D{xAq)}, la,x,[n] = D--Y.i\- (1-259) 2. Смещение независимого переменного в области оригиналов. Если x(g) = D{vW}, D{xln ± к}} = e±x{q). (1.260) Если п < к, то D {х [и - Л]} S 0. 3. Изображение разностей. Если начальные условия нулевые и x{q) = D [x\ri\], то D{A*x[fi]} =(««- l)x(). (1.261) 4. Умножение изображений. Если Xi(g) = D{xi[«]}; Хг(д) = Р{х2[п]}, i> I Z [m] Х2 [и - m] = X, iq) х {q). (1.262) 5, Нахождение оригинала по изображению (общий случай). Если x{q)D{x W}, x{q)e"dq. (1.263) 6. Нахождение оригинала по изображению (частный случай - теорема разложения). Если x(q) = H{q)IG{q), H{q) = ao + ae + ...+a„\ (1.264) G{q) = bo+bie +... + b", (1.265) H(gv) (1.266) где g, - простые корни уравнения (1,265), т. е. [ dGiq)/de-]0. Прнмер 1.23. Пусть x()-eV(e«-0- Найдем оригинал, соответствующий этому изображению. Здесь G{q) = e-e = 0 имеет один корень qi = а; [dG(q)/de] = 1. Тогда из (1.266) х[и] = е"-1 0 1 2 3 4 5 6 7 8 9 10 [11] 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 |
|||||||||||