Слаботочка Книги

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 [111] 112 113 114 115 116 117 118 119 120 121

Рис, 7.33. Определение дисперсии ошибки регулирования на ЭВМ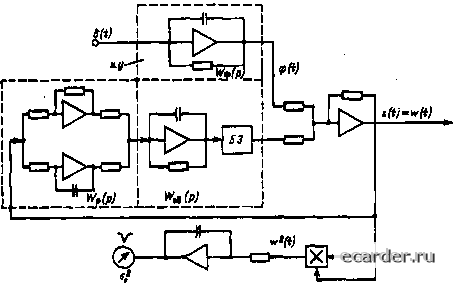

Рис. 7.34. Пример определения af на ЭВМ

Иф(Р) = 0,l/2/(y + р) = + (7.142)

где Гф=1/у. йф = аф/.

Структурная схема решения задачи показана на рнс. 7.33. В качестве примера на рис. 7.34 приведена схема определения и\ на АВМ для АСР с ПИ-регулятором, где

to6(P) = W*V(ro6P+l).

5(c) задается начальными условиями.

Информационный метод

Одноконтурная АСР, изображенная на рис. 7.35, путем простейших преобразований

г-п г-п if .

Рис. 7.35. Структурная схема одиоконтурной АСР

приводится к виду, показанному на рис. 7.36. В этом случае ее можно рассматривать как замкнутый канал передачи информации у [16].

С информационных позиций точность работы такого канала тем выше, чем больше его пропускная способность

(7.143)

где /=uj/2it; Sif) и (/)-спектральные шютности сигналов x{t) и ф((); об{Ю VVp(Jf)-K4X объекта и регулятора; F = = "среа/Зл - частота среза S{f).

В ниформациоиной теории управления для оптимизации рассматриваемой снстемы применяют критерий = макс, который при нормальных видах одномерной плотности распределения вероятностей x{l) н ф(1) совпадает с критерием минимума дисперсии оишбки регулирования.

Для АСР с ПИ-рея улятором при = = макс оптимальные параметры настройкн

Рис. 7.36. Преобразованная схема одноконтурной АСР

Со и Cj находят аналитически из совместного решения системы уравнений [16]

F + (dco/dci ~ co/ci) arctg [(Ci/Cq) f ] = 0.

(7 144)

где первое уравнение определяет в аналитической форме границу области заданной степени колебательности АСР.

Для определения величины F используют уравнение

{f)df=acjl,

(7,145)

где а - достаточно малое число, зависящее от точности определения S{J) в реальных условиях и заданной точности решения поставленной задачи.

Например, для многих процессов корреляционную функцию Kp{z) в доверительном интервале 0,laj с доверительной вероятностью 0,9 можно аппроксимировать выражением

К,(т) = ае-1*1. (7.146)

Если на основании принятых соображений принять я = 0,05, то из (7.145) и (7.146) имеем

F = 2y. Метод максимума АЧХ

(7.147)

Поясним метод на примере АСР с ПИ-регулятором. Последовательность расчетов в этом случае следующая (рнс. 7.37):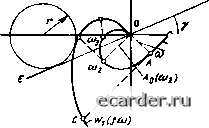

Рис. 7.37. Построение границы области заданного запаса устойчивости АСР по методу максимума АЧХ

1) вычертить WoQiJoi) и задать несколько

частот ш;

Шь 012, . "й™, (7.148)

2) для каждой из частот со, провести вектор {j<Oi) (вектор OA и аналогичные ему на рис. 7,37);

3) по частотной харак lepHCTHKe объекта Woefyio) построить семейство частотных характеристик разомкнутой системы для fcp = 1 и нескольких значений Тиз;

(Ум) = (1 - J/T„,<o) (;ш). (7,149)

Для этого следует значений Т„,: T,. 7-„j2

задать несколько

потом каж-

дый вектор ИобО";) При частоте ш, повернуть на угол 90° и разделить на (оТ. Получится ряд новых векторов, аналогичных АС и соответствующих частотной характеристике разомкнутой системы прн и = и, и Т = = Т,. Точки С, соединить плавнмми кривыми;

4) провести прямую ОЕ под углом

Y = arcsin (1/М); (7.150)

5) Путем подбора провести окружность с центром па оси абсцисс и радиусом г, касающуюся одновременно прямой ОЕ и Wi{j(d) для данного Ги;

6) для заданного коэффициент передачи регулятора

fcp = M/[(M2-l)r], (7.151)

где г Определяется согласно п. 5;

7) построить ло результатам расчета в плоскости кр - кр/Таз (или кр - Тиз) границу области заданной степени колебательности АСР. Дальнейшие расчеты по определению ошимальной точки на этой границе аналогичны приведенным выше.

7.4. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ПАРАМЕТРИЧЕСКОЙ ОПТИМИЗАЦИИ

Эти методы в большинстве своем основаны на прямом контроле переходных или часто1ных характеристик АСР в процессе подбора оптимальных параметров настройки рег)ляторов. Сначала регулятор включают в работу с произвольными параметрами настройкн, обеспечивающими устойчивое движение АСР. После этого наносят возмущения (например, с помощью задатчика) и

наблюдают реакцию системы на эти возму-шения. Целенаправленно изменяя параметры настройки регулятора по заранее известному алгоритму, добиваются нужною вида переходного процесса или определенного положения некоторых точек КЧХ в комплексной плоскости.

Обычно это многошаговая итерационная процедура, поэтому эти методы часто называют итерационными. В настоящее время они разработаны настолько, что позволяют в ряде случаев автоматизировать процесс параметрической оптимизации АСР и осуществлять его при минимальном участии че:ювека-наладчика. Вопросы автоматизации настройки с помощью итерационных методов освещены в специальной литературе, например в [20], поэтому здесь они не рассматриваются,

Настройка АСР по методу «отработ1Ш вoзIvщeння за одно включение»

Этот метод применяют при наладке АСР с малоинерционнымн объектами регулирования, подверженными большому влиянию помех, когда ана:[итические методы малоэффективны из-за чрезвычайно неточных сведений о динамических характеристиках обьекта.

На первопачальпом этапе наладки ПИ-регулятора проверяют цену деления задатчика. Для этого переключатель рода работ переводят в положение -.Автоматическое» и наносят небольшие возмущения задатчиком в обе стороны, наблюдая за изменением регулируемого параметра. За цену деления принимают среднее из трех - пяти опытов. Стабилизируют процесс. Переключатель управления ставят в положение «Автоматическое» и задагчиком наносят возмущение, допустимое по условиям технологии.

После nepeoio включения регулятора переключатель управления ставят в положение «Дистанционное» и наблюдают за регулируемым параметром. Если параметр, установленный регулятором за одгго включение, меньше (больше) заданного, то коэффициент усиления регулятора мал (велик). Изменяя кр, добиваются точной отработки возмущения за 0Д1Ю включение.

После выбора кр повторяют опыты с изменением задания при различнь[х 7„з, но после первого включения регулятора переключатель управления оставляют в положении «Автоматическое» и наблюдают за направлением дaJ[hнeйiuиx срабатываний регулятора. Если регулятор продолжает вклю-

чаться в ту же сторону, что и при первом включении, необходимо увеличить Тцэ, в противном случае - уменьшить. Корректировка Тиз продолжается до тех пор, пока последующие включения регулятора после первого не будут отсутствовать.

Метод Цнгл>и н Ннкольса

Замкнутую АСР с П-регулятором (или ПИ-регулятором, превращенным в П-регуля-тор за счет установки бесконечно большого значения Тц) путем постепенного увеличения кр выводят на границу устойчивости. Для этого режима определяют tpp и Т„ер - период установивпшхся автоколебаний, по которым и рассчитывают оптимальные параметры настройки регулятора.

Для П-регулятора

fcp.oHT =0,55tp,,p. (7.152)

Для ПИ-регулятора

р.опт = 0,35fcpKp, 7"и:, Q[T = lj25Tnep.Kp- (7.153)

Метод достаточно прост, он позволяет обеспечить в системе заданный запас устойчивости, но не гарантирует экстремума показателя качества регулирования (интегрального, дисперсионного и т. и,).

Пошаговая оптимизации с оценкой нереходнсж характеристики на каждом шаге

Сущность метода основана на взаимосвязи между формой переходных процессов при различных настройках АСР и расположением соответствующих точек в плоскости параметров настройки АСР. В плоскости параметров настройки ПИ-регулятора существуют линии одинаковой степени i/ (рис, 7.38, а). Из рис. 7.38, а видно, что одну и ту же степень затухания можно получить прн различном сочетании параметров настройки регулятора. Однако другие показатели качества регулирования - максимальное динамическое отклонение, длительность переходного процесса и площадь под кривой переходного процесса - будут при этом различными. На рнс, 7.38, б показан примерный вид переходных процессов для различных точек линии i/ = 0,75. Если в плоскости параметров настройки ПИ-регулятора для заданного построить интегральную оценку качества регулирования (2.70) - (2.72), то она будет иметь вид, показанный на рис. 7,38, е.

Таким образом, если путем изменения настройки регулятора двигаться слева напра-

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 [111] 112 113 114 115 116 117 118 119 120 121