
 | |
|
Слаботочка Книги 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 [117] 118 119 120 121 тора: G2h„ = ul,r/iRi + R2) = 150V3600 = = 6,25 Дж/с. Так как при выключении регулятора в объект будет поступать некоторое умень-HieHHoe количество энергии Cihh, то прн достаточно длительном выключении регулятора температура в печи в установивгпемся состоянии снизится только до некоторого значения Э2нп, которое будет выгпе значения температуры окружающей среды. Для объекта это равноценно неполному оттоку энергии в окружающую среду. В рассматриваемом случае Qiun = = оббгни = 12 6,25 = 75 °С. Таким образом, мы имеем автоматическую систему регулирования с неполным оттоком энергии. Регулирующее воздействие на объект при вьпслючении регулятора = (16,7 - 6,25)/] 6,7 = 0,625. Диапазон колебаний регулируемой величины Ахнп = (0,5 + 0,625) (I - е-""*) + --(0,0102е-°"*) = 0,065, Дхн„ = 0,065 200 = 13 °С. Диапазон колебаний регулируемой величины при неполном оттоке уменьщается на (Дх - Дхн:,) 100/Дх = = (16,6 - 13) 100/16,6 = 21,7 Пример 7.16. В примере 7.15 подключим одни нагревательный элемент непосредственно на напряжение 17авт = 150 В, а регулятором будем отключать и включать только второй нагревательный элемент. В этом случае имеем также систему с неполным оттоком б2ш = 150/1800 = 12,5 Дж/с; Вгш = (16,7 - 12,5)/1б,7 = 0,25. Диапазон колебаний Днп-(0,5 +0,25) (1 - е-*) + -f 0,0102г-°" =0,04. В абсолютных единицах Дхн„ = 8С, Диапазон колебаний уменьшается на 51,7%. Пример 7.17. В примере 7.16 при выходе системы иа заданный режим последовательно с нагревательным .элементом, который включается и отключается регулятором, включается дополнительный нагревательный элемент с сопротивленнем = = = = 1800 Ом. В этом случае будем иметь АСР с неполным притоком и оттоком: Qzm = f/LxAi. + Ri) + vlx/Ri = = 1503600 + 150/1800 = 18,8 Дж/с; BiH„ = (18,8- 16,7)/16,7 = 0,125; В2нп = 0,25. Диапазон колебаний регулируемой величины Дхн„ = (0,125 + 0,25) (1 - е--°) + -ь0,0102е--".= 0,028, Ш1И ДХщ = 5,6°С. Диапазон колебаний уменьшился почти в 3 раза. Пример 7.18. Имеем АСР температуры электропечи с двухпозиционным импульсным регулятором (рис. 7.18). Параметры электропечи как объекта регулирования приведены в примере 7.11. Требуется определить оптимальные параметры настройки регулятора, если известно, что возмущающими воздействиями на систему являются колебания напряжения в сети AU = ±10% и колебания температуры окружающей среды ДЭ = ±10*С. Определим максимальное количество энергии в единщу времени, выделяемой нагревательным элементом при включении регулятора: GlM.Kc = (авт + A[/)/R = = (150 -I- 0,1 150)V900 = 30,3 Дж/с, минимальное количество энергии Ошт = (150 - 0,1 150)/900 = 20,4 Дж/с. Максимальное регулирующее воздейст-вне регулятора при его отключении Bl = (GlManc - бзд1/бзд = = (30,3- 16,7)/16,7 = 0,81, минимальное регулирующее воздействие Выин = (Qimhh - бзд)/6ад = = (20,4 - 16,7)/16,7 = 0,21. Так как в уС1 ановившемся состоянии = k,Q!t, ТО максимальное регулирующее воздействие регулятора при его выключении Вгмакс = (9зд + А9)/9,д = (200 + 10)/200 = 1,05, минимальное регулирующее воздействие Вгман = Фзд - A9)/9m = = (200 - 10)/200 = 0,95. Согласно (7,168) определяем оптимальные параметры настройки регулятора: = 0,21/1,05 - 0,2; рпт = 0,95/0,85 = 1,17. При запаздывании в объекте = = 4 мин и числе полных циклов за время запаздывания, равном, например, п = m = 5, по (7.162) находим выдержки времени и t2 генератора импульсов: г, = 4.60Д(1 + 0,2) 5 - 0,2] = 41,4 с; (2 = 4-60.а2/[(1 +0.2>-5-0,2] = 8,2 с. По (7.164) находим выдержки времени tj =4.60/[(1 + 1,17)-5 - 1,17] = 10 с; U = 4 60 1.17/[(1 + 1,17) 5 - 1,17] = 29 с. Пример 7.19. Определим диапазон колебаний регулируемой величины (температуры) АСР с двухпозицнонным импульсным регулирующим устройством. Объект имеет передаточную функцию вида (7.157), ке = 1, 76 = 5 мин, = 2 мин. Регулирующие воздействия регулятора Bi = 0,5; Bi = 1. Заданное значение температуры = 500 °С. Параметры настройки регулятора следующие: а =0,3; = 1,3; п"т = 10. По (7.161) находим положительную амп-интуду колебаний температуры: xlhmh = 0,5(1- g 5(10 + 0.3- 0ад 1 20р 0,5 1-е 5 12.7 , 5-.3,7 2 10 1.3 (10-t) = 0,018. По (7.163) находим отрицательную амплитуду: \ - е 5 10+ 1,3 10- 1,3 1 5 21,7 , 21,7 1* к= I 5 21.7 0.039. Диапазон колебаний температуры Дл:„„п = 0,018 -I- 0,039 = 0,057, 0,057 500 = 28,5 X, Если для данного обьекта применить простое двухпозиционное регулирование, то даже при статической характеристике регулятора без зоны неоднозначности диапазон колебаний температуры Ад: = к(В, + Вг){\ - е"**) = = (И-0,5)(1-е -) = 0,495, Ад: = 0,495-500 = 248 "С. Таким образом, при двухпозиционном импульсном регулировании диапазон колебаний температуры уменьщается почти в 9 раз. 7.6, МОДЕЛИРОВАНИЕ АСР НА АНАЛОГОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИНАХ Моделирование на АВМ является эффективным средством исследования АСР, особенно со сложной структурой. На модели можно предварительно просмотреть различные варианты АСР с различными параметрами настройки н оценить качество регу-лирования. Линейная АВМ, иа которой решаются линейные дифференциальные уравнения, состоит из усилителей постоянного тока с глубокой отрицательной обратной связью. Передаточная функция такого усилителя W{p)=-ZIZ„ (7.169) где 2о - полное сопротивление цепи обратной связи; Z] - полное сопротивление входной цепи. Полное активное сопротивлеине Zr = R. (7.170) Полное сопротивление емкости С Zc=yCp. (7.171) Пользуясь понятием полного сопротивления на линейных усилителях, можно смоделировать звеио с любой Передаточной функцией. Так. например, если Zo = Zc = = 1/Ca а Zi = Z« = л, to Wlp) = - /Zi = - ЩСр = - l/Tp (7.172) и усилитель моделирует интегрируюпее звеио с постоянной времени Т = RC. Если R - в мегаомах, а С - в микрофарадах, то размерность Т получается в секундах. При структурном моделировании АСР разбивают на элементарные звенья и каждое звено моделируют с использованием Таблица 7.18. Основные элементы аналоговых вычислительных машин Наименование решающего элемента Структурная схема решающего элемента Сокращенное обозначение решающего элемента Уравнение решающего элемента Сумматор lSx2 tf*jrnO-cm- 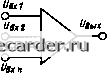 Интегратор l/вх Ri О-cz {> Увых -О Интегратор-сумматор u$Ki Rl o 08x2 Rz O-CZ3 О-CI> Овш -О Увх10- "вхгО- 9хп О-  0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 [117] 118 119 120 121 |