Слаботочка Книги

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 [15] 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

Таблица 2 2 Звенья и наиболее распространенные их соелинения

Структурная схема

Сигнальный граф

Учлоиые уравкеиии сигнального графа

±x, -

w\»-

it, W, IV; Wj ]f2

X, 1 X, W) x„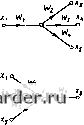

X2 = WXt

X2Xi± W.X4.

X=WiX2

X2=X± Xi X} = WX2

X=Xi± wx

IVi Xi; №"4 Xj

X,= W,XjiW,Xi + + IV2X2 + WX)

(сгрока 4 ia6j[. 2.2) некосредсчвенно из узловых уравнений сиЕнальноЕО [ рафа находим передаточную функцию такой сисгемы

X/Xi = W= WJil ± W.Wi),

анало(ичную получепаой ранее [см. (2.38)].

При сложном сигнальном графе с большим числом узлов систему можно рассчитать методом последовательного упрощения топо.тогни сети графа путем замены последовательных, параллельных или встречно-параллельных ветвей одной ветвью с результирующей передаточной функцией (см соот-ве[С[венно строки 2 - 4 1абл. 2.2).

Устойчивость АСР

Под устойчивостью системы понимается ее способность возвращаться к состоянию ус1 ановивЕНС! ося равновесия после устранения вошуЕцения, HapyiHHBiuero указанное равновесие.

Для линейных АСР решение уравнения их движения (2 15) имеет вид

У (О = У(0св + (Овын,

где - вынужденная coc[aвJ[яюl[aя ре-

шения уравнения (2.15), определяемая видом х(г); у (t)cB - свободная составляющая решения уравнения (2.15), определяемая корнями

р, характеристического уравнения "пЛ" + OiP"" + ... + а„ = 0.

(2.40)

Магематически условия устойчивости формулируются в виде

limjCOci. =0. (2.41)

Поскольку

yit),, = t С,еР, (2.42)

где С, - постоянные, определяемые начальными условиями.

Ус I ойчивость линейных АСР определяется только корнями р, характеристического уравнения (2.40) и формулируется в следующем виде; для устойчивости линейной АСР необходимо и достаточно, чтобы все вещественные корни характеристического уравнения (2.40) были отрицате.гьны. а комплексные корни имели отрицательную вещественную часть, т. е все корни располагались в .гевой полуплоскости корней р,

Для уравнений высоких ступеней определение корней характеристического уравнения связано с определеииымн трудностями, поэтому разработан ряд правил (критериев), позволяющих определять устойчивость АСР, не решая характеристическО! о уравнения.

Кригерий Гурвниа. Из коэффициентов характеристического уравнения (2.40) составляется главный определитель Гурвица

«1 «о О

"1

"5

О О

а„-2 й„

(2.43)

по следующим правилам:

1) по [данной диагонали выписывают последовательно коэффициенты уравнения (2.40), начиная с а до й„;

2) столбцы определителя заполняют гак: вверх - коэффициентами с возрастающими индексами, вниз - коэффициентами с убывающими индексами;

3) все коэффициеяты с индексами меньше и больше нуля заменяют нулями.

Система будет устойчивой, если при Яо > О главный определитель Гурвица А, ы все его диагональные миноры Л, будут больше нуля, где Ai определяют по следующим формулам.

Д, =ai; Дг =

«1 Оэ йо аз

: Дз =

а, аз as

(Jo "2 "4

«3

(2.44)

Из критерия Гурвица вытекает следствие: для устойчивости АСР иеобходи<ло. но недостаточно, чтобы все коэффициенты уравнение (2.40) бы.ш больше нуля.

Из сфуктуры построения определителя Д„ следует, что

Д„ = а„Д„.,. (2.45)

Если определитель Д„ i приравнять нулю при положительности всех предыдущих определителей, то получим уравнение, соот-ветсгвующее границе устойчивости-

Д„-1 =0.

(2.4Ь)

Критерий Михайлова. Если в характеристическом уравнении

Dip) = аор" + fljp"" -1-... + а„ (2.47)

заменить р па /о. то получим характеристический вектор

OOM) = aoOw)" + «it/w)

+... +а„ =

= Mi(4)+jN(<a).

(2.48)

При изменении ю оч О до ос конеп вектора £)(/ю) комплексной плоскости вычертит кривую, называемую характеристической кривой или годографом вектора £){Дв). По виду характеристической кривой можно судить об устойчивости АСР (рис. 2.8).

Д..1.Ч устойчивости АСР необходимо и доапаточно, чтобы характеристическая кри-вач при изменении а от О до со, нячав свое движение с положительной веществс}!-ной полуоси, последовательно прошла п квадрантов комплексной плоскости, нигде не обращаясь 6 нуль (здесь п -степень характеристического уравне}П1я}, Как следствие из критерия Михайлова вытекает, что для устойчивой АСР корни уравнений М(ш)=0 и д(ш) =0 должны чередоваться.

Крк1ерий Ыайквиста. Этот критерий позволяет судить об устойчивости замкнутой АСР по КЧХ разомкнутой АСР.

Условимся о следующем. Ecjm при изменении «) от О до X КЧХ пересекав! отрезок всшесгвенной ОСИ ( - ср. - I) сверху вниз, то будем счиать это положительным переходом, если снизу вверх - то отри!1ателыплм; ес1!и КЧХ начинается на отрезке аеществен-ной оси (-0С, -1), 10 будем считать это за 0,5 перехода с соотве1СТвующим знаком. При этих условиях критерий Найквиста формулируется слелуюгцим образом: чт4)бы ЛСР была устойчива в замкнутом состоянии, необходимо и достаточно, чтобы при измгнгиик т от до lyj разность между числом положительных и отрицательных переходов КЧХ

Рис. 2.8. Годографы вектора D (ja) для устойчивых (a) и неустойчивых (б) систем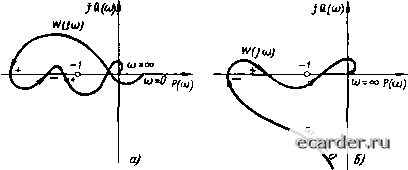

Рис. 2.9. Примеры КЧХ АСР, устойчивых при m = 2 (а) и ш » О (б)

р(1Эол)кмутом АСР через отрезок вещественной оси {-со, -1) равнялась т/2, где т - число корней характеристического уравнения разомкнутой АСР, находящихся в правой полуплоскости плоскости корней р, (рис 2.9).

Опэбнсте. Рассмотренные критерии позволяют судить об устойчивости АСР при заданных значениях ее параметров. Однако в практике часто возникает задача, когда несколько параметров АСР можно изменять в Определенных пределах, чтобы обеспечить ие только устойчивость системы, но и *адан-иые ее качестаениые показатели.

Случай 1. Пусть в характеристическом у[>авненнн

."-14.. . + а„ = О

аор" + «ip"

(2.49)

все коэффициенты заданы, кроме одного или его части к, тогда уравнение (2.49) можно разрешить относительно К:

откуда

>.Q(P) + R(P) = 0.

1=-R(j>)/Q{p).

(2.50)

(2.51)

Отобразим в плоскость X мнимую ось jta гшоскости корней р, (т е. границу области

устойчивости), для чего в (2.51) заменим р на jm.

X (,ю) = - й (7ю)/е (/(о) = х{ь>)+ jy (to). (2.52)

Изменяя ш от О до оо (при отрицательных частотах получается симметричная кривая), построим в плоскости X границу области устойчивости (рис, 2.10). Так как при изменении fl) от -сс до -hoc область устойчивости в плоскости корней лежит слева по ходу хшиження, то, штрихуя D-кривую в плоскости X слева, при изменении ю от - со до + оо получае.ч искомую область устойчивых-значений X, окруженную £)-крнвай с внутренней

Рис. 2.10. 1>-разбненяе плоскости одного параметра

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 [15] 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121