
 | |
|
Слаботочка Книги 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 [16] 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 штриховкой. Поскольку нас интересуют лшпь вещественные значения "К, искомые значения X будут представлять собой отрезок вещественной оси, лежащей в устойчивой области Случай 2. Пусть в характеристическом уравнении (2.49) заданы все коэффициенты, кроме ц и Х, предположим также, чю в уравнении (2.49) не! ни произведений \iX, ни их степеней выше первой, т. е. уравнение (2,49) можно разрешить относительно ii я X: \iS{p) + XQip} + R(p) = 0. (2.53) Отобразим мнимую ось jm плоскости корней характеристического уравнения (2.49) в плоскость коэффициентов \к-Х, для чею в уравнении (2.53) заменим р на US Ow) + >-Q Offl) -I- Л Ofi>) = 0. (2 54) Отделяя мнимую и вещественную части в (2.54), получаем сисгему из двух уравнений uSi (to) + XQi (ш) -I- Ri (ш) О ;) iiSi (w)+\Qi((fl) + R2H=0,J (2.55) откуда (2.56) Si (co)GiH S2(u))e2(fi)) Л, = -Ri(fi>)Gi(fi>) -2(fi))G2(fi>) S, (0)) - Л, (ffl) S2 (ш)-К2(а,)1 (2.57) Задавая ш значения от -со до +-оо, по (2.56) строим D-кривую в плоскости д - X (рис. 2.11); D-кривая несимметрична относительно осей, но точки для положительных и отрицательных <о совпадают. Выражения (2.56) определяют только одно значение для ц и >. при каждом поло-жигельном или отрицательном to только  тогда, котда эти уравнения совместны и линейно независимы. При некоторых значениях со - со, уравнения (2 56) перестают быть линейно независимыми (в частности, всегда при е)=Ояе) = ±со). В этом случае одновремеи-но Л) (илн Л}) и Л оказываются равными нулю ичи бесконечности Это означает, что одно из уравнений (2.56) является при данном значении <а = <а, следствием другого и тогда в плоскости ц - Х появляется не точка, а прямая - так называемая особая прямая. Поэтому граница £>-раэбие11ИЯ должна быть дополнена особыми прямыми. Если А = О при всех со. ю D-кривой не существует и D-разбиение производится особыми прямыми. Правила штриховки D-кривой и особых прямых (см. рис. 2.11): 1) D-кривую штрихуют двойной штриховкой при изменении со от О до со слева, если А > О, в справа, если Д < 0; 2) особые прямые при (й = О и со = ±со штрихуют одинарной штриховкой, так чтобы одновременно заштрихованные или одновременно н&(ашгрнхоЕанныс стороны прямой н кривой располагались встречно. Особую прямую при (о =е (о, (со, ФО, 0), ?б ± со) также штрихуют, но двойной штриховкой, если в точке пересечения ее с кривой А меняет знак; если знак Д не меняется, ю эту особую прямую не штрихуют. Переход в плоскости ц - Х через двойную штриховку означает переход в плоскости корней р, двух корней через ось /со; переход через одинарную штриховку - переход одного корня через ось Jco. Случай 3. В характеристическом уравнении (2.49) ц и >. связаны нелинейно, т. е. имеются произведения и их степени выше первой В этом случае, заменяя р иа )to и отделяя вещественную и мнимую части, получаем два уравнения вида А(со.Ц,?.)=0, jzi<u,ix,X) = 0. (2.58) Изменяя (о от -со до -t-oo, по точкам строим D-кривую в плоскости р - Правила штриховки в этом случае le же, что и в предыдущем, но D-крнвая и особые прямые штрихуют уже ощнарной штриховкой в зависимости от знака якобиана: (2.59) Рис 2.11. D-разбиепие плоскости двух параметров Запас устомпвости. Из-за неточного знания, а также возможной флюктуации коэффициентов а, в уравнении (2.49) АСР рас-считьтается таким образом, чтобы в ней всегда был обеспечен некоторый запас устойчивости. Теоретически эго выглядит следую-
}а((о) Рис 2.12. Задание запаса уст ойчивос ги в плоскости корней характеристического уравнения 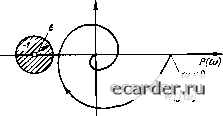 Рис. 2.14. Задание запаса устойчивости по критерию Найквиста 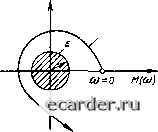 А ((О) Рис. 2.13. Задание запаса устойчивости по критерию Михайлова щим образом: нужно так рассчитать АСР (наладить), чтобы при возможных изменениях коэффициентов а, в уравнении (2 49) корни его не прнближа:[ись к мнимой оси ]{й ближе чем на в&ничину а (рмс 2.12). Задание величины а обычно определяется достоверностью наших знаний о динамических свойствах объекта регулирования и возможными (ожидаемыми) их изменениями. Если устойчивость АСР рассчитывается по критерию Гурвнца, то граница области заданного запаса устойчивости определяется из выражения ,А„-1 =s, (2.60) Где £ > О - величина, задаваемая аналогично а. Запас устойчивост и по Михайлову и Найквисту формулируется в виде требований cooTBeiCTBCHHo к Dijai) и разомкнутой системы: они не должньг заходить в опасную зону радиусом е (см, соответственно рис. 2.13 и 2.14) Достаточно часто об устойчивости .АСР судят по ампл и i удно-частотной харак i е-ристике Л (со) замкнутой системы. Если при (л=(йр А (Юр) терпит разрыв, то АСР вы\о-дит за 1раницу устойчивости Для задания запаса устойчивости необходимо потребовать, чтобы (рис. 2.15) Л(а)р)М(0)М, (2.61) 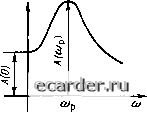 Рис. 215 Амплитудно-частотная характеристика замкнутой АСР [де значение М обьгчно выбирается равным 1Д-2,4, наиболее часго полатаюг М = 1,62 [24]. Качество регулнровавня Любая промышленная АСР кроме устойчивости должна обеспечить определенные качественные показатели процесса peiy-лирования. Качество процесса регулирования обычно оценивают по переходной характеристике hf{t) по отношению к единичному ступенчатому возмущающему воздействию (рис. 2 16). Основными показателями качества являются: время ретулирования, тгереретули-роваиие, колебательность и установившаяся ошибка. Вречя регулирования. Временем регулирования fp называется время, в течение которого, начиная с момента приложения воздействия на систему, отклонения значений регулируемой величины A/i/(r) от ее установившегося значения hfo = i/(x)) будут меньше наперед заданного значения ео- Таким образом, время регулирования опреде-тяет .[ЛИ гельнос! ь (быстродействие) ттереходного процесса. Перерегу шрование Перерегулированием а f называется максимальное от кл онение Ломаке регулируемой величины от установившегося значения hf, выраженнсх; в процентах по отношению х hj-o-  Рис. 2.16. Показатели качества регулирова-нвя Колебательность системы характеризуется числом колебаний регулируемой величины за время регулирования (р. Если за это время переходный процесс в системе совер-таег число колебаний меныие заданного по условиям технологии, то считается, что систе-.ма имеет требуемое качество регулирования в части ее колебательное!и. yimuHoeueuiancn ошибка. В общем случае установившаяся ошибка Eq или ючность регулирования определяется как разность двух значений - уС1 ановившегося рсЕулируемой величины h(, после окончания переходною процесса и заданного д- to = 9о - Ло- (2.62) По отношению к возмущающему воздействию ео = -К- (2.63) Показатели качества регулирования опреде-1яю1ся непосредственно по кривой переходною процесса, которую можно получить эксперименгально илн решением дифференциальных уравнений системы Решение дифференциального уравнения является трудоемкой задачей, в связи с -зтим в инженерной практике находят широкое применение косвенные оценки качества регулирования Косвенными оценками называются некоторые величины, в той или иной .мере характеризующие отдельные особенности переходного процесса. Косвенные оценки качества ршулнрова-пая. Одной из косвенных оценок качества регулирования яв,1яв1ся степень удаленности корней характеристического уравнения замкнутой системы от .мнимой оси (рис. 2.17) Расстояние а б.!ижайшего корня от мнимой оси характернзуе! lanac устойчивости системы, называется степенью устойчивости этой сис1емы и равно веществеииой части корня, ближайшего к мнимой оси. Наибольший из углов (р, образованных о[ринательной вешествсиной полуосью и лучами, проведенными из начала координат 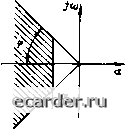 Рис 2.17. Область расположения корней с заданными значениями а и ф чере! корни, характеризует колебате 1ьность системы Котангенс это1 о угла т = ctg (р называется степенью колебательности. Согласно (2 42) комплексно-сопряженные корни, имеющие максимальный угол (р, ;1адут составляющую колебательного переходною процесса, имеющую наименьшее 1атуха1ше, и, следова1ельно, колебательность системы будет определяться этой составляющей, так как остальные сос1авляющие имеют большее затухание Для оценки колебательности в ряде случаев удобно также пользоваться понятием «степень затухания». Степенью затухания i]( называется отношение рашости двух соседних амплитуд одного знака кривой переходною процесса к большей из них. Так, для переходного процесса по рис 2.16 V = (АА,ма.с - АЛп)/Лй/м..с (2.64) Степень колебательности и степень затухания связаны .меж>1у собой соотношением v, = ] е 2-г™ 2.65) Чтобы система обладала заданной колебательностью, все корни характеристического уравнения до1жны вписываться в угол 2(р (рис. 2.17). Таким образом, для одновременного обеспечения заданных значений быстродействия и колебательности системы необходимо, чтобы все корни характеристического уравнения лежали внутри заштрихованной области иа рис. 2.17. Для определения параметров системы, обеспечивающих заданные значения а и ф, можно воспользоваться методом i7-pa36He-нйя. Для поС1роеиия i)-кpивoй при определении параметров системы, обеспечивающих заданное значение ot, в (2 S1) и (2.S3) необходимо заменять р не на j<o, а на -oi-i-fio. При определении параметров, обеспечивающих заданное значение (р, необходимо р заменять на ш (/ ~ ") Произведя D-разбиеиис по одному или двум интересующим нас параметрам, можно получить условия, при 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 [16] 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 |