Слаботочка Книги

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 [17] 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

которых система будег обладать заданными быстродействием н колебательностью.

При оценке качества по расположению корней характеристического уравнения можно исходить из следующих соображений. Предполагая, что переходный процесс в основном определяется ближайшим к мнимой оси вещественным корнем (или ближайшей к мнимой оси парой сопряженных корней),

можно найти допустимое значение степени устойчивости с учетом желаемого времени регулирования fp, по истечении которою отклонение регулируемой неличины уменьшится в « раз относительно начального отклонения т. е.

а = Inn/(j

(2.66)

Так, есЛи у (1р) = 0,05ун. то и = 20 и выражение (2.66) примет внд

а = 3/Гр. (2.67)

Если, например, по условиям технологии требуется, чтобы прн ко1еба1ельном переходном процессе амплитуда кажуюго последующего отклонения регулируемой величины уменьшилась в k раз по отношению к амплитуде предыдущею отклонения, то требуемая степень затухания с01ласно (2.64)

ф = (2.68)

Решая совместно (2.65) н (2.68), находим m»Infc/(2n). (2.69)

Если, например, по условиям технологии [ребуется, чюбы каждая последующая амплитуда колебаний переходною процесса уменьшалась в 10 раз по сравнению с предыдущей, го в зтом случае к = ](), степень затухания i/ = 0,9, а степень колебательности m = In 10/2п = 0.336

Интегральные методы онен1еи качества регулирования. В основе этих методов лежит предположение, что качество peiулирования тем выи1е, чем меньше площадь между кривой переходного процесса и заданным значением регулируемой величины, так как эта площадь косвенно харак1еризует потерн на регулирование (рис. 2.18). Наиболынес применение находят инте1ральные оценки слелуюц1ею вида:

/2= Je {t)dt; о

(2.70)

(2.71)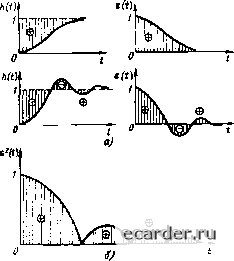

Рис. 2.18. Геометрическая интерпретация интегральных оценок качества регулирования

/з= Ге

dt, (2.72)

где е(г) - отклонение параметра от заданною значения (ошибка pei улврования); Т- постоянная времени некоторой экспоненты, по которой желате-пьно изменение переходного процесса адя данной сипемы.

Минимизируя указанные интегралы, можно получить тс значения параметров (коэффициентов дифференциального уравнения АСР), которые обеспечивают наилучшее качество pei yjmpoeaHHH.

HHTcipaji (2.70) определяет собой алгебраическую (т. е. с учетом знаков) сумму площадей, ограниченных кривой переходного процесса и заданным значением регулируемого параметра, Поэтому он может быгь npHMCHeii только адя оценки неколебательных монотонных процессов h{t) (рис. 2.18, а). Качество колебательного переходною процесса h{l) (рнс 2.18,6) лучше оценивать интегралом (2.71) или (2.72).

Частотные методы оценки качества регулирования. Этн методы базируются на гфе-образовании Фурье н на том, что переходный процесс при заданных возмущениях однозначно связан с видом КЧХ замкнутой .ЛСР. Таким образом, по частотным характеристикам можно судить о качестве переходного процесса.

Наиболее часто в частотных методах нсследовання АСР в качестве возмущающего

воздействия применяется единичная ступенчатая функция, определяемая выражением (2.19). Разложение этой функпии в непрерывный гармонический ряд осущест вляется с помощью интеграла Дирихле;

sm at

dm. (2.73)

Если КЧХ замкнутой АСР имеет вид W{]) = P{a)+jQUi>), (2.74)

то реакция системы на возмущение в виде единичной ступенчатой функции (2.73) (переходная функция) может быть вычислена по формулам

h{t) =

Р(а))

sin to/ d{u; (2.75)

Л(/) = Р(0)

Q(to)

cos 0)1 d(U .

(2.76)

Выражения (2.75) и (2.76) лежат в основе частотного метода исследования качества переходного процесса при единичном вошу-щении вида (2.19); пользуясь любым из них, можно составить предварительное приближенное суждение о качестве регулирования:

1) приблизительно одинаковым Р{са) соответствуют приблизительно одинаковые hit);

2) для двух сходных (to) и Р2(со). отличающихся только масштабом по оси to, т, е. Рг (nto) = Pj (ш), переходные процессы отличаются только масштабом но оси г, т. е.

h,it/n) = h2(t); (2.77)

3) в установившемся состоянии

й(со) = Р(0); (2.78)

4) чтобы hit) стремилась к установившемуся значению, необходимо, но недостаточно соблюдение при всех to неравенства

] Р (to) I < Р (0); (2.79)

5) если Р (со) изменяется по монотонно убывающей кривой / (рис. 2.19), для которой Р (ш) > о, Р (to) < О, Р" (со) О, то это означает, что параметр С1ремится к установившемуся значению без перерегулирования, а длительность переходного процесса

Гр%47г/со„,, (2.80)

где {j)oi ~ верхняя граница области суще-

Рис. 2.19. Монотонная (/) и колебательная (2) пействитепьиые частотные характеристики замкнутой АСР

ственных частот адя данной системы (эффективная ширина спектра [25]);

6) если Р (to) имеет вид кривой 2, то

fpn/cooj; (2.81)

7) если Р (со) обращается в бесконечность при некотором значении ш, то АСР неус-юйчива;

S) продолжительнос1ь перехо;1ното процесса будет тем меньше, чем более пологий характер имеет Р((о).

Если необходимо уточнить представление о качестве регулирования, то следует построить h (t) no выражению (2.75) или (2.76). Применявшиеся до недавнею времени [ipn-блгиженные меюды вычисления h{t) ао Р(со) (например, метод трапепеидальных частотных характеристик) в сяаш с бурным развитием средств вычислительной техники в настоящее время потеряли практическую ценность.

Оценка качесгва pei ушрования при случайных входных воздействиях. Если на вход АСР воздействует случайный процесс X it), то на се выходе возникает тоже случайный процесс Yit), связанный с входным процессом соотношением

У(г)= ? wi)X[t-)d, (2.82)

где н () ~ импульсная переходная характеристика системы.

Эту формулу следует рассматривать в том смысле, что появление на входе АСР рештизацин х (f) случайног о процесса X it) приведет к появлению на ее выходе реализации y{t) случайного процесса Y{t).

Для стационарного входного воздействия кoppeJrятиt>ннaя функция случайного процесса на выходе

fyi-)= ? ?w()w(Ti)A% (-л-Ьт)л,

- ю - ж

(2.S3)

где (т) - корреляционная функция случайного процесса на входе АСР

Качество регулирования а таких системах обычно опенивают величиной дисперсии процесса на вь[Ходе = <if, которая получается иэ (2.83) при г = 0:

aj= ] ] w{i,}wm)KA~)iic,dy. (2,84)

Если входное вочдейсгвие - белый шум [K,(T) = 5(x)l, то

ctJ = I (1) dt.

(2.85)

Вычисления можно упростить, ес;1и оперировать не с корреляционными функциями входа и выхода, а со спектральными плотностями Sj;((o) и Sj,((o). В этом случае

.?,(ш) = SЛa))И(,a.)! , 1 ?

(2.86)

Sv (со) dm =

1 Г

5Л"))1 WOwjli/co, (2.87)

где I (/{0)1 - амплитудно-часто гная функция системы [модуль КЧХ VF(/oj)].

2.3. ЛИНЕЙНЫЕ ДИСКРЕТНЫЕ СИСТЕМЫ

Основные понятия н определения

Дискретными называются системы, в которых осуществляется передача и ггреобразо-вание СИ1 налов, квантованных по уровню или по времени. Квантование по уровню соответствует замене действительного значения преобразуемого сигнала в любой момент времени его дискретным значением, кратным целому числу уровней квантования. Квантование по времени соогветствует замене непрерывного во времени сигнала его значениями в дискретные равноотстоящие моменты времени. В зависимости от вида квантования различают следующие дискретные АСР:

а) релейные, в которых происходит квантование по уровню; эго, как правило, нелинейные сисгемы. они будуг рассмотретгы в § 2.4;

б) импульсные, в которь[х происходит

квантование по времени; эти системы рассматриваются в настоящем параграфе;

в) цифровые, в которых происхо.хит квантование тто уровню и времени, при малых значениях квант уемот о сиг на,ча, когда квантование по уровню сказывается существепно, цифровая система сводится к релейной, при больших !наченИях квантуемого сигнала, когда дискретностью по уровню можно пренебречь, цифровая система сводится к импульсной.

В импулт>сных системах квантование по времени осуществляется импульсным эле-MCriTOM (ИЭ), выходная величина которого представляет собой модулированную ттосле-довагельность импульсов (рис. 2.20), Различают следующие типы импульсной модуляции (рис. 2.21):

а) амплитудно-импульсную модуляцию (АИМ), при которой изменяется амплитуда Л выходных импульсов в зависимости от значений входной величины в дискретные равноотстоягцие на величину Т моменты времени;

б) широтно-импульсную модуляцию (ШИМ), при которой изменяется ширина импульса {Т в зависим ост и о г значений входной величины в дискретные равноотстоягцие моменты времени;

в) время-итульсную модуляцию (ВИМ), которой соответствует опредатенный временной сдвиг F.T импульса постоянной формы в зависимос1и oi значения входной величины в дискретньге равноотстояшие моменты времени.

Каждый тип модуляции характеризуется так называемой крутизной характеристики ИЭ:

Аим=-4А; шим = УТА; кшм=Т/х. (2.88)

Если величина к постоянна и ие зависит от X, то импульсный элемент линейпый, если и непрерывная часть (рис 2.20) линейна, то система называется линейной имг1у]гьсной.

Уравнения движения

Разомкнутые импульсные системы. Эти

системы в общем случае могут бьтть пред-CTaBJTCHH ггоследовате;[ьным соединением ИЭ и НЧ (см. рис. 2.20). Анализ таких систем целесообразнее всего производить в относительном времени l = t/T= n, используя дискретное преобразование Лапласа и сохраняя при этом те же удобства, которые имеет обычное преобразование Лапласа при решении диффepeнтиaJтьньтx уравнений.

Представим импульсный элемент ИЭ в виде последовательного соединения простей-

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 [17] 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121