|
| |
|
Слаботочка Книги z(t) Рис. 2.20. Структурная схема разомкнутой импульсной системы: ИЭ импульсный элемент; НЧ - непрерывная часть 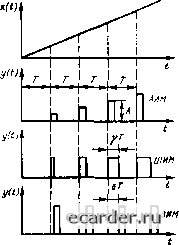 Рис. 2.21. Виды импульсной модуляции x(tn y(t) Рис. 2.22 СI руктурная схема импульсного злемента Г пнч~[ -!----- Рис. 2.23. Преобразованная структурная схема разомкнутой импульсной системы шего импульсного элемента ПИЭ и формирующею элемента ФЭ (рис. 2.22). В простейшем импульсном элементе непрерывная функция X (t) преобразуется в решетчатую yi{t) или в относительном времени t = n Л[л] преобразуется в У] [н], Формирующий племен 1 ФЭ нз ординат решетчатой функции Ух ["j формирует импульсы определенной формы в зависимости от типа импульсной модуляции; ФЭ для линейных импутьсных элементов в динамическом отношении может быть представлен передаточной функцией ]ф(р) и-чи Л-я относительною времени 1 = п- передаточной функцией {q), коюрая получается нз Wip) по выражению (2.89) где р = qfT. Непрерывная часть ЕЧ ана.ю1 ично также может быть представлена передаточной функцией Wq)- Объединим ФЭ и НЧ в [ак на1ываемую приведенную непрерыв- ную часть ПНЧ с передаточной функцией тЧ)=Щ{ч){ч). (2.90) тогда pajoMKHyiBH импульсная система в простейшем случае будет представ.тять собой последовательное соединение ПИЭ и ПНЧ (рис. 2.23), для которой z(q, B) = x{q) W{q, е). (2.91) Здесь W(q, е) есть D-нреобраювание Лапласа для импульсной переходной характеристики W In, е] ПНЧ: W{q, e) = D{w [п. е]) = .£ w [п. е] е (2.92) 11 = 0 Отличительной особенностью выражения (2.91) является то, что л [и] опредсчена лишь для дискретных моментов времени ( = п [аналогично x{q) = D {х [п]}], а г [п, с] находится для .чюбого мумеюа времени t = n + E, 0<Е<1. Если приведенная непрерывная часть содержит элемент запаздывания (в ФЭ или НЧ), то его передаючная функция равна Рис. 2.24. Структурная схема замкнутой импульсной системы е"" или е , где т = т/Г-относитадьное запаздывание. Тогда W{q,ii) = e-4W{q,z), (2.93) где Жо (д, е) - передаточная функция ПНЧ без запаздывания, Относительное запаздывание х всегда можно представить в виде x=m + xi, (2.94) где т - целое число; О < < 1. В этом случае W{q, е) =€"""Ио(«, e-Ti) прн Ti < £ < 1: (2.95) W{q, е) = €-<"**Жо(«, 1 + е ~т,) при о < Е < Ti. (2.96) Замкнутые импульсные системы во мио-гил случаял могут быть приведены к схеме, анало! ичной изображенной на рис. 2.24. где /(() - внешнее воздействие. Для дискретных относительных моментов времени г = п г (9); (2.97) n4) = x{q)W{q), (2.98) откуда x{q)nq)l\.\ + W{q)\. (2.99) Подставив (2.99) в (2.91), получим ураз-неинс движения замкнутой системы в виде г(ф е) =nq) W{q, е)/[1 + W(q)\ ; (2.100) здесь {q, Щ = W{q, е)/[1 + W{q)] (2.101) - передаточная функция замкнутой импульсной системы; G{q) = l + W{q) = о (2.102) - характеристическое уравнение замкнутой импульсной системы. Устойчивость Ешш известны f{q) и K{q,E), то выходная величина z [п, е] может быть найдена по формуле обращения J{q)K{q,B)e"dq. (2-103) Решение (2.103) состоит из двух слагаемых : с] =2-вы„[я, е] + -vE". е], (2.104) где 2нын С". ~ вынужденная составляющая, определяемая видом /[н]; z(»[n, е] - свободная составляющая, определяемая корнями qy характеристического уравнения (2.102). Если с течением времени za [и, е] стремится к нулю, т. е. lim Zcb[«, t] = о. то система называется устойчивой. Обычно 2св[«.в]= i Cv (2.105) (2.106) где i - порядок характеристического уравнения (2.102); Cv - постоянные коэффициенты, определяемые начальными условиями. Из (2.106) следует, что условие (2.105) всегда выполняется, если корни имеют отрицательные вещественные части. С учетом периодичности функции е" окончательно условия устойчивости формулируются в следующем виде: система будет устойчивой, если корни qy характеристического уравнения (2.102) лежат в левой полуплоскости плоскости корней в полосе шириной 2п (заштрихованная полоса иа рис. 2.25). Вычисление корней уравнения (2.102) - довольно трудоемкая задача. Поэтому для выяснения устойчивости системы аналш ично тому, как эю дeлaJЮcь для непрерывных систем, пользуются специальными критериями. Ниже рассматриваются различные формы критериев устойчивости, которые являются аналогами критериев для непрерывных систем. Алгебраический критерий устонивости. Характеристическое уравнение (2.102) можно Рис 2.25, Графическая иллюстрация условий устойчивое ги в плоскости q = Req + j\mq Рис. 126. Графическая иллюстрация условий устойчивости в плоскости г "= с* = а --;Р представить в виде G iq) = бое + ble" i>9 + ...+&, = О (2.107) или, заменяя на z, в виде G{z)=hoz + biz- + .. + ft,=0. (2.10S) Отобразим заштрихованную полосу плоскости q = Req +jlmq на рис. 2.25 в плоскость z = е" = а + j. Граница этой области найде1ся из условия Reg = 0; \mq = = w; z = е/й = ё, + ) sin Й = a + УР, откуда a= + P= = lzl = l, (2.109) т. е. заштрихованная полоса плоскости q на рис. 2.25 отображается в крут единичного радиуса на плоскости z = с* (рис. 2.26). Таким образом, для устойчивости системы необходимо и достаточно, чтобы корни характеристического уравнения (2.108) лежали внутри заштрихованного круга, т. е. чтобы их модули были меньше единицы: z<l. (2.110) Существует ряд методов, позволяющих найти соотношения между коэффициентами Ь, уравнения (2.108), при которых выполняются условия (2,110). Эту задачу можно решить, например, с помощью кри1ерия Гурвица. Для этого отобразим круг единичного радиуса плоскости z в левую полуплоскость нового комплексного переменного = и +jv. Такое отображение может быть осуществлено преобразованием (рис. 2.27) = (z-H)/(z- 1), (2.111) откуда 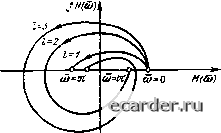 Рис. 2.28. Графическая иллюстрация аналога и:ритсрия устойчивости Михайлова Подставив (2.112) в (2.108), найдем + ai = 0. (2.113) 2 = W-1). (2.112) Для уравнения (2,113) можно применить критерий Гурвица и по (2,46) найти границу области устойчивости в функции коэффи-писнтов й„ однозначно связанных с коэффициентами уравнения (2.108). ялог критерия Михайлова. Подставив в характеристическое уравнение (2.107) q = jib, получим так называемый характериспшче-ский вектор G (/6)) = А/ (ш) + jN Щ. (2.114) При изменении частоты » от О до л конец этого вектора в комплексной плоскости Л/(ш)-7/V(») опишет кривую, называемую характеристической кривой. Для устойчивости системы необходимо U достаточно, чтобы при изменении частоты to от О до п характеристическая кривая (2.114), начав свое движение с положительной действительной оси, последовательно прошла 21 квадрантов комплексной n.iocKocmu против часовой стрелки (рис. 2.28), где / ~ порядок характеристического уравнения (2.107). Аналог критя Найквиста. Если в передаточную функцию (2.90) подставить q - уа>, то получим комплексную частотную функцию W(jui) = P{a)-\-lQm. (2.115) При изменении 6 от О до тс конец вектора (2.115) в комплексной плоскости  Рис. 2.27. Отображение круга единичного радиуса плоскости г в полуплоскость С 
Рис. 2.29. Графическая иллюстрация аналога критерия устойчивости Найквиста Купить офисную бумагу www.bereg.net. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 [18] 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 |