Слаботочка Книги

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 [21] 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

(2 153)

здесь (1) и (2) у ki относятся к первому (2.149) и второму (2.150) способам вычисления ki.

Расчеты показывают, чго при выборе Л] по первому и второму способам в корреляционной функции выходного сигнала получаются односторонине ошибки разных знаков, поэтому в качестве целесообразно использовать

(2.154)

Совместная гармоническая и статистическая линеаризация. Часто входной сигнал z(t) нелинейного звена представ;[яют суммой синусоидального сигнала и случайной функции X (():

z(t) = Asmm + xit) = -4smco£ +т + x{t). (2.155)

В этом случае применяют совместную гармоническую и егатистическую лгшеариза-цию, т. е. заменяю! характеристику не.ти-иейггого звена у(0 =f[z{t)] приближенной

у(ОУо +n,>lsine)/ +ti24cos(af + T]x(i), (2.156)

линейной относительно синусоидальной и центрированной случайных составляюших входного сигнала.

При нечетной характерис1ике y=j{z)

/о = Пот,. (2.157)

Значения т]о, rii, и Л можно определить различными способами нз условия правильного учета передачи нелинейным звеном полезного сигнала, первой 1армоники и уровня флюктуации входного сигнала

Предположим, что »t, и Од изменяются достаючно медленно и нх можно считать постоянными хотя бы в пpeдeJ[ax одного периода синусоида-тьного колебания входного сигнала, Изложенным выше способом проведем статистическую линеаризацию, в результате которой получим

У(Г)«Л + М(0- (2.158)

Из-за наличия периодической составляю-щей в математическом ожидании входного сшнала значения j% и А, оказываются периодическими функциями времени, следовательно, к ним можно применить гармоническую линеаризацию

/S =/о (т, -Ь .4 sin шг, о,) «!Уо {А, moj V

-Ь rii (/4, т„ jAsmmt -Ь г\2{А, т, CT;,).4cosmf,

(2.159)

/о (А, т„ ст,) = ~

/S(m, -Ь А%т (y;,)d<;

(2.160)

Пг (Л m„ ст= - fl{m-\-Asm,o)aud; пА J

х\2(А, т, ст,) =

(2.161)

fU>fix + simli, Ox)cosv;rfi/;

(2.162)

Ci = л (4, fn, CTjc) я= . - ilm* -ь sinv;, aj,)d;

(2.163)

Если известна (p(x) ~ одномерная функ-ция гыотносги распределения вероятности, то на осяованяи предыдущего раздела о статистической линеаризации имеем

/8= J(x + Asm)4>(x)dx,

- со

+ А sm ф) ф (х) dx - Wif

(2.164)

(x-m)f(x + Asmi)(p(x)dx?-. (2.165)

Исследование систем

Мета/i гарионнческою баланса позволяет оценигь усюйчивость нелинейных систем, определить амплитуду и частоту авгоколеба-ннй, а также выбрать корректирующие цепи, обеспечиваюгцие заданные характеристики нелинейных систем. Возможность применения этого метода к стационарным сис1емам определяется близостью пернодическо! о jutn-жения системы к гармоническому. Это условие обычно удовлетворяется, когда линейные части системы являются фильграми низких

частот, т. е. хорошо отфильтровывают высокие гармоники.

Предположим, что нелинейная система состоит из линейной части с комплексной частотной функцией ИдОш) и нелинейного безынерционного звена с комплексным гармоническим коэффициентом усиления Wa {А) Пусть в этой системе возникли автоколебания с частотой сОа и амплитудой А, тогда согласно критерию Найквиста

W„0<)lV„(A)=-U (2.166)

или, обозначив

M„(A)=W;(A),

(2.167)

условия возникновения автоколебаний запишем в виде

(2.168)

Для определения частоты со и амплитуды Ла автоколебаний решение (2.168) удобно проводить графически. Для jtoi о построим (рис. 2.42,(1) в комплексной плоскости ()Сй) я - (А). Если они пересекаются, то в системе возможны автоколебания, если не пересекаются, то автоколебания невозможны. Параметры автоколебаний и А определяются точкой иеражчения lVj(a) и -М„(А): по W-,{)to) и А по -Мп{Л).

Если Wa(jGi) И -Мя{А) пересекаются в нескольких точках (рис, 2.42,6), то это свидетельствует о том, что в системе возможны автоколебания с различными параметрами (ш и А),

Определение устойчивости автоколебаний производится по следующему правилу: если W„ (/О)) при изменении со от О до сс охватывает часть -Ма(А), соответствующую увеличению амплитуды, то автоколебания неустойчивые, в противном ciynae - устойчивые.

Р(а>) ut,

рис. 2.42. Графический метод определения параметров авгоколебаняй в нелинейной системе

Руководствуясь этим правилом, можно заключить, что ИЗ трех автоколебаний на рис. 2.42, lj и б устойчивым будут только автоколебания в первой точке на рис. 2.42,6 с параметрами ш,1 и А.

Метод статнстическЫ! линеаризации. Рассмотрим нелниейную систему, изображенную на ряс. 2.43, где ср - нелинейное звено с характеристикой

2 = (р(у). (2.169)

Ж(р) - передаточная функция линейной части системы.

На вход АСР поступает стационарный случайный процесс я (£) с математическим ожиданием т, и дисперсией <s\. Необходимо определить характеристики выходного сиг-пала у ((): математическое ожидание ту и дисперсию <з\.

Произведем статистическую линеаризацию нелинейной характеристики (2.169), используя формулу (2.146):

z(r)=fcom,p + ci(0, (2-ПО)

где коэффициенты fco и fc] в обшем случае являются известными функциями пока неизвестных величин Жу и Оу;

fco = to ("V у). 1 = (fny. y)- (2-171)

Таким образом, в результате статистической линеаризации нелинейное звено заменяется безынерционным усилигелем с различными коэффициентами усиления полезного сигнала Шу и помехи (() Передаточные функции линеаризованной системы для полезно! о сигнала и помехи имеют вид

{р) = W{p)l\\ -н Ш{р)\ ; (2.172)

Ф"(Р)= W[l -Hfci»()j- (2.173)

С использованием (2,172) при = const

ту = тЖ(0)/[1 Ц- ко (ту, Оу) И(0)3 . (2.174)

Уравнение (2.174) содержит две неизвестные величины {ту и о,) и поэтому может быть решено только совместно с уравнением, определяющим дисперсию выходной величины.

S,(«)

dta.

(2.175)

Рис. 2.43. Нелинейная АСР

где (ю) спектральная плотность i(f).

Уравнения (2.174) и (2 175) могут быть решены совместно методом последовательных приближений. Для JTOro необходимо задать исходные приближенные {начении ко и ki и вычислить в первом приближении и Сту по (2.174) н (2.175). После этого можно уточнять значения ко» kj н вычислить га, и Оу во втором приближении и т д.

Уравнения (2.174) я (2.175) можно решить рафическим методом Для этого заменим (2.174) равноценной системой уравнений

г\ = ту; (2.176)

Л = m,I(0)/[l + ко (т„ о,) И(О)] (2 177)

Уравнению (2.176) соответствус! биссектриса координатного угла на рис. 2.44, ii в координатах Шу-ц; в этих же координатах уравнению (2.177) соответствует семейство кривых с параметром Оу. Построив кривые, соответствующие уравнению (2.177) juifi ряда значений Оу, и определив точки пересечения нх с прямой (2.176), найдем шачения Шу,, соо гве I ствующие выбранным значениям а,. После зюго 1Ю найденным точкам построим кривую / (рис. 2.44,6) в координатах т, - ст,. В этих же координатах нос i роим кривую 2 по уравнению (2.175). Точка 4 пересечения кривых / и 2 лает искомое решение.

Ииюженный метод применим только к системам, i лв невозможны автоколебания, так как только при их 01сутствии т, может быть постоянной величиной прн постоянном Шх- Поэтому прежде чем примени ii, изложенный метод, необходимо исследовать систему на возможность возникновения в ней автоколебаний, что можно сделать методом т армонического баланса. Если нсслсдование покажет, что в системе возможны устойчивые автоколебания, то для определения ее точности необходимо применять метод совместной статистической и гармонической линеаризация,

Метод фазовых траекторий. Состояние динамической системы, описываемое лиф(}}с-

ренциальными уравнениями «-Г0 порядка, в каждый момент времени определяется значениями ретулируемой величины и (л - 1) ее производных. Это лае! возможность представить в некотором и-мерном пространстве состояние системы в каждый момент времени Отдельной точкой - так называемой ии>6ражающей точкой. Процесс изменения состояния сис1емы представляется как некоторое движение июбражающей точки, точнее - как ее траектория, так называемая фазовая траектория. Совокупность фазовых траекторий составляет фазовую картину систе.мы (фазовый портрет системы).

Для практических расчетов полыование MHOI омерным фазовым пространством свя-iano с определенными трудностями, поэтому при anaJTHie нелинейных систем обычно ограничиваются двухмерной фазовой плоскостью, В этом случае по оси абсцисс откладывают значение регулируемой величины V (ее отклонение от установившегося состояния), а по ося ордина! - 1начение Z = dy/dt.

Состояние АСР, описываемое уравнением НС выше второ! о порядка, в каждый момент времени определяйся значениями у и г и может быть охарактеризовано положением точки М на фазовой плоскости (рис. 2 45). В переходном процессе значения у и Z будут изменяться и, с 1едова1ельно, изображающая точка М будет 5анима1ь различные положения на фазовой плоское! и По траектории этой точки можно су;1ить о характере переходного процесса.

Если у - отклонение pei улируемого па-раме 1 ра от установившегося значения, то для устойчивых систем в установившемся состоянии у = О и г = О, следовательно, фазовые траектории устойчивой АСР при t со должны стремиться к началу координат, а фаговые траектории неустойчивой АСР при I ос должны удаляться от начала координат. Точки фашвой плоскости, где сходятся (илн откуда расхоля1Сн) фазовые траектории, называются особыми точками*.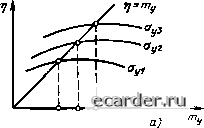

/77у/ /77у2 /77yJ

Рис. 2.44 Графическое решепне уравнений (2.174) и (2.175)

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 [21] 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121