
 | |
|
Слаботочка Книги 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 [22] 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 y(t) (2.178) 6} У Рис. 2 45 Характеристики состояния динамической системы: о - во временной области; б - на фазовой плоскости В параметрической форме фазовые ipa-ектории описываются системой уравнений dyldt = P(y, г);] dzldt = Q(y, Z),. где Р (у, z) к Q (у, z) - нелинейные функции у н 2. Разделив второе уравнение системы (2.178) на первое, получим дифференциальное уравнение фазовой траектории dz/dy = Q (у. г)/Р (у, Z) = Я (у, z). (2.179) Раз.те.1ин переменные и проинтегрировав (2.179), получим выражения для семейства фазовых траекторий. Для определения устойчивости АСР ачедуст рассматривать поведение фазовых траекторий в окрестностях особых точек (в данном случае - в окрестности начала коорлина!). Для этой пели линеаризуем систему уравнений (2 178), т е. разложим их в ряд Маклорена, и офаничимся двумя первыми членами, в результате получим dy/dt = ау + bz; (2.180) dz/dt = су + dz, (2 181) тде а = гр/ду; Ь=сР/дг; с dQ/dy; d = = cQ/dz прн у = z = 0. Решив (2,180) и (2.181) относительно у, получим линеаризованное уравнение движения системы в окрестностях особой точки: у"-(a+d)y+(ad-bc)y = 0. (2.182) Повсценяе системы в окрестностях особой точки определяется корнями характеристического уравнения - {а т d)p + {ad - be) =0 (2 183) Например, если корни уравнения мнимые, т. е. pi.j = ijw, то у (f) = 4cosmr; (2.184) г(1) = y[t) = -А<о&1пШ. (2.185) Возведя в квадрат (2.184) и (2.185) и сложив, получим уравнение фазовых траекторий в виде уУа +zyAW = I. (2.186) Это - уравнение эллипса. Переходный процесс и фазовая траектория для этого случая изображены на рис. 2 46. Особой точкой, которая носит название центр эдесь является начало координат. Отметим, что незатухающим колебаниям у{1) (автоколебаниям) на фазовой плоское I и соо I не тст вуют фазовые т раек тории в виде эллипсов; другими словами, наличие замкнутых фазовых траекторий на фазовой плоскости свидетельствует о возможности возникновения автоколебаний в АСР. Различные случая особых точек, их названия, соответствующие ям переходные процессы и фазовые траектории приведены в табл. 2.4, где /-3 - различные переходные процессы и соответствующие им фазовые траектории на фазовой njmcKociH. Приведенные в табл. 2.4 фазовые траектории справедливы только для определенной области у - Z, в которой допустима линеаризация системы уравнений (2.178). За пределами этой области в силу существенного отхода от лииейньЕХ соотношений в исходных временных уравнениях фазовые траектория будут иметь тачсствсиио иной характер Для тех нелинейных АСР, у которых С]а1ические характеристики нелинейных звеньев могут быть разбиты на линейные участки [см. (2.124) - (2.130)], можно построить фазовые траектории отдельно для каждОЕО ;шнейн010 участка, а затем соединить (припасовать) их друг с друюм Рис. 2.46. Пере-ходный процесс (а) и фазовая траектория (б) для автоколебаний 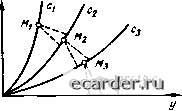 Рис. 2.47. Построение фазовых траекторий методом изоклин Таблица 2.4. Особые точки Название Переходный процесс ФdJoвыe траектории Устойчивый фокус  Неустойчивый фокус -Af- Устойчивый узел 
Неустойчивый узел  Седло  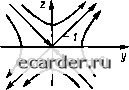 Построение фазовых траекторий нелинейных АСР можно выполнить также методом изоклин с использованием уравнения (2.179). Для этого сначала на фазовой плоскости строят линии, соответствующие алгебраическому уравнению Н (у, z) = с = const. (2.187) Каждому значению с (рис. 2.47) соответствует своя линия, называемая изоклиной. Изоклина - это геометрическое место точек с одинаковым наклоном фазовых траекторий, проходящих через этн точки, т, е. для точек изоклины dz/dy = с = const. (2.188)  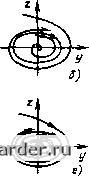 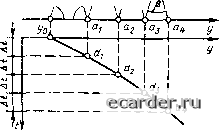 Рис. 2.48 Разновидности предельных циклов: а - устойчивый; 6 - полуустойчивый; в - неустойчивый, г - два предельных цикла Рис. 2.49. Построение переходного процесса по фазовой траектории Используя свойство изоклин (2.188), фазовые траектории строят в следующем порядке. Берут произвольную точку Mi на изоклине Ci и из нее проводят две прямые до пересечения с изоклиной Cj. Первую прямую проводят под углом arctgci, соответствующим углу наклона фазовых траекторий в точках изоклины су Вторую прямую проводят под углом arctg соответствующим углу наклона фазовых траекторий в точках изоклины Ci. Точка Мг на изоклине С2 находится как середина пересечения изоклины с2 С обеими прямыми. Далее аналогичным образом из точки Mi проводят две прямые с углами наклона arctg Cj и arctg сз до пересечения с изоклиной Сз, на которой находят точку Мз. Hociynaa аналогичным образом, находят ряд точек М„ соединив которые, получают фазовую траекторию АСР. Отличительной особенностью фазовых портретов нелинейных АСР является наличие в них замкнутых фазовых траекторий, называемых предельными цикшми, которым соответствуют автоколебания. Предельные циклы бывают устойчивыми, полуустойчивыми и неустойчивыми. Устойчивым предельный цикл соответствует устойчивым автоколебаниям, он характеризуется тем, что фазовые траектории накручиваются на него с обеих сторон (рис. 2.48, й). Полуустойчивый предельный цикл характеризуется тем, что фазовые траектории накручиваются на него с одной стороны и скручиваются с другой (рис. 2.48,6). Для неустойчивого предельного цикла фазовые траектории скручиваются с него с обеих сторон (рис 2.48,в). Фазовый портрет нелинейных ЛСР может иметь несколько предельных циклов (рис. 2.48, г). Фазовый портрег нелинейных АСР, описываемых дифференциальными уравнениями ие выше второго порядка, дает полное прел1-ставление о динамике нелинейной системы при детерминированных воздейс1виях, включая точность, устойчивость и качество регулирования. По фазовой траектории можно по-строить переходный процесс Для этого поступают следующим образом (рис. 2.49): а) вычерчивают фазовую траекторию; б) выбирают временной шаг At построения у (О = У ("At), где и - целое число; в) определяют уюл р 2 arctg(Ar/2); ij Hi точки y(t) = yo, определяемой начальными условиями, проводят прямую под углом а - 90" - р/2 до пересечения с фазовой траекторией в точке 6; д) из точки 6i проводят прямую под углом р до пересечения с осью у в точке а , е) точку а, проецируют в плоскости y[t) в T04fty di, ж) из точки Й! проводят прямую под углом = 90" - р/2 до пересечения с фазовой траекторией в точке bi; з) из точки Ьг проводят прямую под углом р до пересечения с осью у в точке «г; и) точку Oj проецируют в плоскости y[t) в точку di, поступая аналогичным образом, находят точки d, искомой y(t). По построенному таким образом переходному процессу y(t) можно достаточно объективно оценить качество регулирования в нелинейной АСР при различных начальных условиях. Ice «\ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 [22] 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 |