
 | |
|
Слаботочка Книги 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 [24] 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 следует провести оцифровку шкал органов настройк-и регулятора, Кроме opi анов настройки, непосредственно изменяющих коэффициент дифференциального уравнения регулятора, регуляторы, как правило, имеют также органы настройки, косвенно влияющие на эти коэффициенты и изменяющие параметры статических характеристик регулятора или режимы его работы, например органы настройки, изменяющие чувствительность регулятора, демпфирование входного си мала, длительное)ь импульсов при релейно-им-пульсном способе формирования закона регулирования н т. п. Параметры регулятора, (ависящие от [шложения этих органов настройки, также на!ываются параметрами настройки регулятора. В качестве примера таких параметров настройки регулягора можно назвать «нечувствительность регулятора Адч», «постоянную времени демпфирования 7дф», «дJгитeльиocть импульсов Д1имг1** и т. д. Регуляюр вида (3.2) имеет один параметр настройки «коэффициент передачи ку,», С учетом (3.2) КЧХ разомкнутой системы (3.1) запишется в виде W(i(a) = kpWijia). (3.3) Из (3,3) следует, что при подключении к объекту такого регулятора КЧХ объекта увеличиваются иа каждой частоте пропорционально в kj, раз. Пропорциональные регуляторы сокращенно на1ываюг П-регуля-т opa\f и. В динамическом отношении П-ретуля-тор является усилительным звеном (см. § 2.2). Передаточная функция П-регулятора (3,4) На рис, 3,1 приведены КЧХ paiOMK-нутых систем с П-регулятором. При р=1 КЧХ разомкнутой системы совпадает с КЧХ объекта peryjrnpoeaHHH При кр>1 КЧХ разомкнутой устойчивой системы приближается к точке В (-1.0), при кр<1 КЧХ отходит от этой точки На рис. 3,1 в качестве примера изображены две КЧХ разомкнутой системы: при кр = kpi = 1,5 и при кр = кр2 = 0. В cooiBeiciBHH с (3 3) на рис. 3.1, например, вектор ОЕ2 КЧХ разомкнутой системы равец OE2=kpOA2=i,50A2, где ОЛ - вектор КЧХ объекта. Переходные процессы в П-регуляторе описываются выражением (3.5) где е - входное воздействие на pei улятор, равное отклонению регулируемой величины от заданного значения; ц - воздействие регулягора на объект, направленное на ликвидацию отклонения регулируемой величины от TaiiaHHoro значения. При настройке П-регулятора следует иметь в виду, 41 о чрезмерное увеличение запаса устойчивости с ухудшает качество регулирования, так как при этом затя1ивае1ся переходный процесс в систоле [увеличивается время регулирования (см, § 2.2)], увеличиваются динамическая ошибка и устагю-вившаяся ошибка pet улирования по каналу как задающего, так и возмущающе! о воздействия. С учетом этого для системы с П-регуля-тором имеется определенное оптимальное значение коэффициента его передачи А,р, которое и следует выбира i ь при настройке системы. Интегральные регулеторы Передаточная функция замкнутой АСР по каналу регулирующего воздействия (рис. 3.2,6) Фр(р) = Ир(р) Wo6(p)/[I + Wp(p) Wip)l (3.6) По каналу возмушающего воздействия (рис 3.2, в) со стороны регулирующего органа Фг{р)=Щ{р)/11 + \Ур(р)}обШ (37) По (3-6) и (3,7) можно установить, что при статических объектах и регуляторе АСР будет статической по каналу как задающею, так и возмушающего воздействия. При астатическом обьекте система будет астатической по каналу задающет о воздействия и статической по каналу возмущают цего воздействия. Таким образом, АСР с П-регулятором всетда имеет установившуюся ошибку регу-лирования по каналу во1мущающего воздействия, а при статическом объекте - и по каналу задающего воздействия. Хотя, как указывалось выше, путем выбора оптимальною значения коэффшщента передачи П-регулятора можно существенно уменьшить установившуюся ошибку регулирования, ее полная ликвидация в систеые с П-регулятором даже теоретически невозможна. Структурная схема замкну!ой системы по каналу ошибки регулирования представлена на рис. 3,2, г. Переда! очная функция системы на рис. 3.2, г Фв(р) = 1/[1 + Ир(р)Иоб(Р)]. (3.8) Чтобы в установившемся режиме (г-* со, р 0) отсутствовала установившаяся ошибка регулирования, необходимо выполнить условие Фе(р)р.о-0< I.e. Фе(0)=0 Из (3.8) следует, что ij>g(0)=0 при Ир(;)ИобН-.0- Так как в общем случае коэффициент <а„ О в выражении (2.29) передаточной функции объекта (объект статический) и, следовательно, (,6(0)5 со, то для выполнения yCJ!0- вия Жр (0) Иоб (0) = «5 необходимо, чтобы при р=0 передаточная функция Ир(О) была равна Ир(О) = со. Таким образом, для этого требуется применение в системе астатического регулятора с законом pei улирования, 0!1ределяе-мым передаточной функцией Жи(р) = Ш!и В 6oJ!ee o6i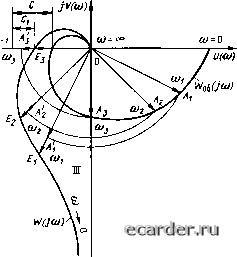 Из (3.12) следует, что в системе с И-регулятором вектор КЧХ объекта на дайной ча- Рис. 3.3. Комплексные частотные характеристики объекта У/ (jro) и разомкнутой АСР У/{Щ с И-регулятором Передаточную функцию И-регулятора часто записывают в виде (см табл. 2 1) (i.B) 1ле Гя - постоянная времени интегрирования - параметр настройки регуляюра. Рассмотрим физический смысл постоянной времени интегрирования. Закон И-рсгулирования И-регулятора с учеюм (3.13) запишется в виде (3.14) Предположим, что на вход регулятора поступил постоянный СИ! нал ь = Ер. При этом выходной сигнал в соотве1е1вии (3.14) будет изменяться по закону й = е 7"„. По истечении времени t = значение выходного сигнала будет равно ц = €о. Таким образом, постоянная времени интегрирования И-регулятора равна времени, в течение которою с момента поступления на вход регулятора посюянною си(нала сигнал на выходе регулятора достигнет значения, равного значению входного сигнала. Дифференциальные регулирующие устройстве Про1Юрииона.чьные регуляторы оказывают иа объект су/цес(вемное регулирующее воздействие, когда ретуируемая величина уже имеет значительное отклонение от la-данною Значения Интегральные ретуляторы оказывают регулирующее воздействие, постоянно наращивая его по интегральному закону Таким образом, П- и Й-регулягоры не могут упреждать ожидаемые отклонения ре-гу.тируемой величины, peai ируя только на уже имеющиеся в данный момен! нашения 1ехноло1ического процесса. В то же время если регулируемая величина в какой-го момент времени начинает быстро отклоняться от заданно! о значения, то очевидно, что па объект nocrynwjJH значительные возмущения и что отклонения регулируемой величины в результате этого воздействия будут нaчИieльньIMИ, В этом случае жела!ельно иметь регулятор, который вырабатыва т бы регулирующее воздействие, пропорциональное скорости отклонения регулируемой величины от заданного шачения: Передаточная функция регутятора Ид(р) = 7>. (3.16) Такой регулятор при большой скорости отк.чонения регулируемой величины, когда в начальный момент П-регулятор оказывает слабое рыулирующее воздействие на объект, а И-регулятор только начинав! наращивать регулирующее воздействие, оказывал бы существенное регулирующее воздействие на обьелт, ликвидируя тем самым ожидаемое отклонение ре1улируемой величины, причем чем больше возмущающее воздействие на объект, тем быстрее будет отклоняться регулируемая величина от заданного значения и тем значительнее будет регулирующее воздействие peiyJiHiopa (3.15) на объект, направленное на нейтрали!а[1ию возмущающего воздействия с учетом изложенных соображений для нелей автоматического регулирования и введены в практику регулирующие устройства, формирующие закон pei улирования, пропор-ционачьный скорости огкчонения регулируемой величины (3.15). Рсали{ацня (3 16) в чистом виде практически неосуществима. В связи с зтнм в качестве Д-регулнруюших устройств используются дифференциаторы с законом регулирования Td\i/dt + ц = k,Tdp./dt (3.17) с передаточной функцией 11ропорцноналыю-штегральные регуляторы Для комплексного использования преимуществ законов П- и И-регулирования в автоматических системах широко применяются pei уляюры, формирующие законы как П-. так и И-pei улирования одновременно. Такие регуляторы называются про-порционально-иптегральными или сокращенно - ПИ-pei уляторами. Пропорционяльно-интегральные регуляторы оказывают воздействие на регулирующий орган пропорционально 01клонению и ин1е1ралу от отклонения регулируемой величины. sdt. (3.19) \i=T,-ydz/dt. (3 15) Передаточная функция ПИ-регулятора WnHip) = kp + l/Tp. (3.20) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 [24] 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 |