
 | |
|
Слаботочка Книги 0 1 2 3 4 5 [6] 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 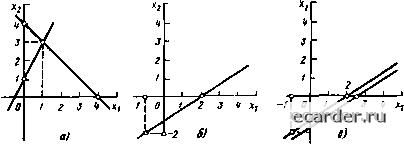 Рис. 1,7, Геометрическое предсшвление системы двух уравнений а-система определенная, 6 - система неопределенлая, е - система несовместная числом неизвестных, введем понятие «-мерных векторов (или точек «-мерною пространства). Выше были введены понятия двух- и трехмерною векторов. Было показано, что, например, каждому двухмерному вектору а соответствует пара чисел <xi и «з, взятых 8 определеииом порядке. Вектор я с координатами (Xi и 0(2 записывает ся в виде я = («1, «г)- Аналогично определяется трехмерный вектор a=(ai, «2, otj), или, что то же, точка в трехмерном пространстве, Двух-в трехмерные векторь[ геометрически изображаются с помощью радиусов-векторов; при этом координаты вектора представляют собой аггебраическис проекции радиуса-вектора на оси прямоугольной системы координат. Используя понятия двухмерного вектора, решение jcj = а, и Хг = системы двух уравнений с двумя неизвестными можно тракт OBaib как двухмерный вектор х - = (а[, 1X2). Вместо того чтобы говорить о двух неизвестных и Xj, можно говорить о неизвестном векторе X = (xi, Лг)- Например, решение первой системы уравнений примера l П можно записать в виде х = (1,3). Поня1ия двух- и трехмерного векторов примем как исходные для дальнейших обобщений. Будем называгь п-мерным вектором а (или ючкой п-мсрного пространства) совокупность п чисел «1, аг, at,,, взятых в определенном порядке, и запишем его в виде а = ai, ..., з„). Числа а,.....а„ называются координатами вектора а. Применительно к автома! ическим системам управления 1шня гие н-мсрного вектора быJro проиллюс1рировано иа примере рис 12, Все математические зависимое г и векторного йсчнсгения, изложенные выше, сгграведливы и для «-.мерных векюров. Используем понятие «-мерпых векторов для упрощения записи системы .чинейных уравнений (1.116) Введем для этою ш-мер- пые векторы ai =(aib Д12. , Omi); Яг «гг.....я«г); У (1.118) а„ = (ai„, Дг......a«J, , координаты коюрых представляют собой коэффициенты при соответствующем неизвестном X во всех т уравнениях системы (1116). Введем также т-мерный вектор - свободный член "о = (ащ, 120, . o„q). (1 119) Тогда систему (1 116) можно записать в виде одною векторного уравнения a,xi -f ajXi + ...+а„х„=Яо, (1-120) решение которого сводится к нахождению таких значений х = ai..... х„ = а„, при подстановке которых в ураввевие (I.I20) получается тождество a,ai + ajKa + ... -Н а„а„ = во- (1-121) Таким образом, если ввести понятие и-мерного вектора х, задача решения системы уравнений (1.II6) сводится к нахождению вектора х = («1, «2. .. , otn). Таким обраюм, введение понятия п-мернот о вектора свело задачу решения системы линейных уравнений к определенным ма гшатнческмм операциям над век юрами. В процессе решения систем уравнений производятся различные тождественные преобразования, целью которых является переход к более простым и удобным систшам перенос hjrenub из одной части уравнения в дру ун), почленное умножение обеих частей уравнения на одни и тот же огличный от нуля мтюжитель, почленчое вычитание из уравнений системы одного какого-либо уравнения, уравнивание коэффициентов при неизвестны), и i, л. Используя понятие и-мерного вектора, все рассмотренные олфапни можно формально трактовать как преобразования векторов Например, рш1ение системы уравнений (1.122) можно рассматривать как преобразование неизвестного вектора х = (xi, xj) в известный ао = (oiO( яао) с помощью известных ком1)фи-циентов Оц, 0(2, 021, Для упрощения записи вводят понятие матрицы преобразования или таблицы чисел, которая для системы (1.122) имеет вид
Соответственно для системы уравпепий азования имеет вид (1 116) матрица преобр "и "12 «21 Й22 "«1 а»2 Матрицу записывают сокращенно в виде II a,i 11 либо обозначают одной буквой А, В и т. д. Если для векторов х и Яо ввести соответствующие матрицы
то систему уравнений (1.116) н матричной форме можно saiiHcaTb в виде I де Ах ао, 021 "22 (1.123) «1» ". Таким образом, отыскание неизвестных х], .., х„ в системе уравнений (1.116) своди гея к определению матрицы вектори х, т. е, к операции над матрицами. Необходимо помнить, что матрица - это таблица m х п чисач. записанных в определенном порядке, и понятие матрицы иель(я оюждествлять с понятием определитель (см. ниже), который является алгебраическим выражением и строится по опреде- ленному правилу из элементов матрицы. Например, мазрица второго порядка имеет вид Оц «12 "2 г «22 а определитель второго порядка «11 12 «2 J 022 = "ll"22 - ai2"21- (1.124) Алгебра матриц Матрицу расоиатривают как математический символ, над которым можно производить действия, аналогичные действиям над обычными числами. Совериенно так же, как с помощью двух вещественных чисел приходят к построению чисел новой природы, а имещго комплексных чисел вида а + jb, так и с помощью m X п чисел, расставленных в виде определенной таблицы, приходят к понятию нового числа - магриец»! и к понятию алгебры матргщ. В отличие от обычной алгебры алгебра матриц имеет одну особенность, которая заключается в иском-мутативностн ум1южения, т. е. результат умножения зависит от порядка coмнoжитeJreй. Виды матриц. Матрица вида «11 ... ui, «21 «22 "2 а«1 ««2 состоящая из m X п чисел, расположенных ь m строк и п столбцов, называется прямоугольной Mamputfeu размером т х п или т X п-матрицси. Числа, составляющие матрицу, называются ее элементами. Еспи т = п, то матрица называется квадратной, а число m - ее т>рядком. Для квафатной матрицы выражение «II «21 «ii «1Я 2» Оя1 «-2 называется определителем (детернинантом). Это Число вычнслясеся по формуле Д = «,1-4,1+«.2-4,2 + - + ",„Л.и. (1-125) где v4,ft - алгебраическое дополнение (или адьюнкт) злемен1а а,: Л„ = (-\ГК,. (1.126) Определитель Д, получае1Ся нз определи-1еля Д путем вычеркнвашгя 1-й строки и it-ro столбца. В (1.125) определитель раскрыт по i-й строке, но он может быть раскрыт н по любому к-му столбцу: Д = fliHu + aikik + •• + «пкЛ*- (I.I27) С помощью выражений (1.125) и (1.127) вычисление любого опредезЕИтеля можно свести к вычислению определителей второго порядка: Sp(A): = ad - cb. (1.128) Если определитель матрицы равен нулю, то говорят, 41 о она вырожденная. Минором матрицы называется определитель, полученный вычеркиванием из матрицы одинакового числа строк и столбцов. Если все миноры порядка г + 1, которые можно составить из магрицы, равны нулю, а среди миноров порядка г хотя бы один отличен от нуля, то число г называется рангом этой матрицы. Например, матрица 3 2 1-1 9 6 3 -3 -6 -4 ~2 2 0 0 0 0 вырожденная, порядок ее равен 4, а ранг 1. У квадратной матрицы имеются главная диагональ, состоящая из элементов и, 22, ,Оип; " побочная, состоящая из элементов а, „, а-щ -1.....а„ i. Квадратная матрица, у которой все недиагональные элементы равны кулю, называется диагональной матрицей, например 10 0 0 0 2 0 0 0 0 5 0 0 0 0 4 Диагональная матрица, все диагональные элементы которой равны единице, называется единичной, в матричном исчислении она играет такую же роль, как число I в обычной алгебре. Если ввести в рассмотрение символ Кронекера I при I = к; О при I ф к. (1.129) то для единичной матрицы (1.130) Сумма диaгoиaJrьныx элементов матрицы А размера п х п называется следом (шпуром) матрицы А и обозначается Тг(А) или Тг(А)= (I.I31] Для единичной матрицы размера п х п Тг(А) = п. (1.132) Матрица, у которой все элементы равны нулю, называется нуль-матрицей; она играет ту же роль, что и число нуль в обычной алгебре. Прямоугольная матрица, состоящая из одного столбца, на1ывается столбцевой, например Прямоугольная матрица, состоящая из одной строки, называется строчной, например а,2 ai„li. Если в квадратной матрице элементы, расгюложенные симметрично относительно I лавной диагонали, равны между собой, т. е. a,t = I о такая матрица называется симметричной, например 1 X ~у X 3 4 -у 4 Z л 4 -3 4 6-2 -3 -Z 9 Матрица, у которой элементы, расположенные симметрично по отношению к главной диаюнали, равны, но противоположны 1Ю знаку \a = -я,), называйся кососиммет-ричнай, например 4 - X 1 Матрица, которую можно получить из исходной, заменив строки столбцами, называется транспонированной и обозначается А\ Например, матрица 2 4 6 А = 7 3 4 8 1 5 является транспонированной по отношению к матрице 0 1 2 3 4 5 [6] 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 |