Слаботочка Книги

0 1 2 3 4 5 6 7 [8] 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

Дисперсия характеризует разброс значений случайной величины X вокруг ее среднего значения.

Величина

<J>=V- (1-155)

называется среднеквадрагтческим отклонением. Эту величину следует отличать от среднеквадратического значения Хср„, которое определяется по формуле

(Хср»=аг= 1 xp{x)dx. (1.156)

Если = О, то Хер KB = а.

Наиболее распространенным распределением для случайных величин является нормальное, для которого

р(х) = -L e-(j-"j/(2aJl (j i57j

Вероятность попадания нормально распределенной случайной величины X в интервал а X b определяется формулой

р(а<<Ь) = Ф[(&-т,)/а-

-Ф[{а-т,)/оД (I.15S)

где Ф (х;) = - = j" е - табулированная функция.

Случайные в№торы

Случайные величины X я Y, рассматриваемые совместно, можно геометрически ингерпретировать как случайную точку с координатами X и У на плоскости х, у или как случайный векгор, направленный из начала координат в точку {X, У). Систему II случайных величин Xi, Хг,...,Х„ можно гакже изобразить случайной точкой или случайным вектором в п-мерном пространстве.

Функцией распределения F{x. у] системы двух случайных величии X и Y называется вероятность совместного выполнения неравенств

F(x.y) = p[(X<x).(y<y)]. (1.159)

Геометрически F(x, у) интерпрсгируегся как вероятность попадания случайной точки {X, Y) в квадрат с вершиной (х, у), заштрихованной на рис. 1.9. Вероятность попадания случайной точки {X, У) в прямоугольник R (рис. 1,10) выражается «крез функцию распределения F(x, у) формулой

р[(х. y)eR] = f(P, 6)-f(a, 5)-

-F(S, Y) + f (а, у), (1.160)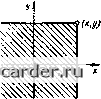

-в X

Рис. 1.9. Геометрическая интерпретация функции F (зс, у)

Рве. 1.10. К определению вероятности попадания точки {X, У) в область R

где знак е означает, что точка [X, У) принадлежит области к. Функция

р(х, y)-5V(x, y)/{dxdy)=F;y(x. у) (1.161)

называв! ся плотностью распределения двух случайных величин X и У и физически предсгавляет собой предел отношения вероят-носги попадания случайной точки в элементарный участок плоскости, примыкающей к точке {х. у), к площади этого участка, когда его размеры стремятся к нулю.

Элементом вероятности для системы двух случайных величии называется величина p{x,y)dxdy, приближенно выражающая вероятность поцадавия случайнее точки {X, Y) в элемент арный прямоу! ольиик со сторонами dx, dy, примыкающий к точке (х, у).

Функция растфеделения F (х, у) выражается чфез плотность распределения;

f{x,y)= ] ] p(x,y)dxdy. (1.162)

- flO - 50

Плотность распределения отдельных величин выражается через плотность распределения р(х, у) формулами

Pi(x)= J p{x,y)dy\ (1.163)

Рг{у) = J P{x,.y)dK

(1.164)

В соответствии с понятиями, принятыми для случайных событий, для системы из двух случайных величин вводятся понятия условных функции распределения случайных величин X л Y [обозначаются Fiixfy) и Fi {у(х)\ и ус-ловных плотностей распределения Pi{x)y) и Р2(у/х):

р(х, y) = pi(x)pj(y/x) или pfx,y)=p2(y)Pi(x/y).

(1.165) 27

Если условный закон распределения одной ш ;1вух случайных величин Л" и Г не зависит от I о1 о, какое значение примет другая, то случайные величины X и У называются независимыми:

Pdx/y)=pi{x); Piiy/x) = Р2(у). (1 166)

Случайные величины X и Уна!Ь[ваются независимыми, если закон распределения каждой из них не зависит от значений, к-оторые принимает другая величина. В про-[ивном случае величины X и Г называются зависим ыми.

Плотность распределения системы не-!ависимых случайных величин равна произведению плотностей распределения отдельных величин, ВХОДЯГЕ1ИХ в лу систему;

Р{х, у] =Pi{x}p2{y)

(1.167)

Важными характеристиками системы двух случайных величин, хо1я и не вполне исчер[[ывающими, являются моменты системы.

Начальным моментом порядка к + s системы двух аЕучайных величин .Y и У называется величина, определяемая формулой

а, = f ] xfp{K, y)dxdv (1.168)

Центральным моментом порчдка к + s системы двух случайных величии А и У называется величина, определяемая формулой

Hi,.= f i {х - m){y-myyp{x,y)dxdy.

(1.169)

Важной характеристикой системы двух случайных величин является цептралыгый момент порядка 1 + 1, т.е. Pii, который назь[вае1Ся корреляционным М1>ме-нтом К, двух случайных величин.

К,, = ц,,1. (1.170)

Для независимых случайных величин Ку:у = 0. Величина

= Ку/а, (1 171)

где = \/d = [/1J2.0 и [/о = /0,2 ,

называется коэффициентом корреляции двух случайных величин Л" и У; он характеризует степень тесноты линейной зависимости между случайными величинами.

Если гу = О, то случайные величины Л" и У называются некоррелированными. Если X и Y связаны линейной функциональной зависимостью вида Y = аХ + Ь, то гу = ± 1, где знак плюс или минус берется в зависимости от знака а. Для любых двух случайных величин II < 1. Для /1вух нормально

распределенных случайных величин X п Y I

Р{х. у) =

X exp

2(1-r,)

(X - т,У

2ry{x - m]{y - m,) (.V - mf

(1.172)

Если две случайньЕС величины некор-релированы {гу = 0) и при згом т = ту, то нормальное распределение принимает кано-нический вид:

р{х, >) =

2ла,ст,

(1.173)

Вероятносгь попадания нормально распределенной случайной точки в прямоу! оль-ник R (рис. 1.10)

р1{х,у)вК] =

6 - m

у - т,

(I.I74)

где функции Ф Ta6yj[HpoBaHbi.

Если для системы п случайных величин (Xj, Х2, --,-Хп) ввести понятие функции распределения как верошности совместного выполнения п неравенств ви;т X, < х,

F(x, Х2, ..,х„) =

-рЦХ, <х,)(Х2 <Х2)...{Х„<х„)1 (I 175)

то аналогично системе двух случайных величин можно ввести понятия плотности распределения, моментов и закона распределения для системы п случайных величин.

Случайные функции

Случайная функция X{t] {вероятностный процесс) - это функция, которая в каждый .момент времени является случайной величиной. То г KoHKpei ный вид, который принимает функция в результате опыга, называется реализацией случайной функ[1ии. Если зафиксировать время, например, в момент ti, то случайная функция (0 обращается в случайную величину Л(Г), называемую сечением случайной функции. Закон распределения F{Xi,{i) сечения X{ti) случайной функции называется одноиерны.и законом распределения случайной функции X{t) Закон распределения системы двух ее сечений X{ti), Л" ((2), представляющий собой функцию че-ibEpex apiyMCHTOB f (xj, t, X2, Г2). называется двухчерпым законом распределения случайной функции X{t).

Для одномерного закона распределения плотность вероятности обозначается p(x,t); для двухмерного p(Xi, ti, Х2, tz).

Математическое ожидание случайной функ11ии X(t) есть неслучайная функция mlt), которая при каждом I представляет собой математическое ожидание соответствующего сечения случайной функции.

Корреляционная функция случайной функции X{t) есть неслучайная функция двух аргументов К(г, /), которая при каждой паре значений t, t равна корреляционному моменту соответствующих сечений случайной функции. При t = f корреляционная функция превращаетсяв дисперсию случайной функции

KAt,t) = aHt). (1.176)

Если распределение системы любого числа и сечений случайной функции X{t) н01»1альное, то случайная функция называется нормальной; характеристики Klt, О и mit) являются для нее исчерпывающими.

Функция

( П =

AtMt) ]/z)(t)Z)x(0

(1.177)

называется нормированной корреляционной функцией случайной функции X{t]. Функция

лy( П= 1 1 Ы1)-тМ X

X [y(()-m,(/)]p(x, у, и f)dxdy (1.178)

называется взаимной корреляционной функцией двух случайных функций K{l) и YU).

Нормированной взаимной корреляционной функцией двух случайных функций Х{1) и >(f) называется функции

(1.179)

Если Rxy{t, t) = О, то случайные функции X{t) и Y{t) называются некоррелированными. Если

Z(r)-X(f)+ y(f),

(1.180)

m,(t) = mAi) + mj(0; (1.181)

+ R,(Kt) + R,Al,f). (1.182)

Если математическое ожидание случайной функции 1л,(0 = = conbt, а корреляционная функция зависит только от разности между своими аргументами х =1 ~ t, i.e. Кх [t, f) = (т). то такой случайный процесс

называется стационарным. Существует подкласс стационарных случайных процессов, называемых оргодиче(кими, для которого среднее по .множеству (т. е. математическое ожидание т) с вероятностью, равной единице, равно среднему по времени:

а. =т,= lim

x{t)dt. (1.IS3)

Среднее по вршени квадрата функции lx{t)-m,y

М(Гх(0 - тЛ} = lim

(1.184)

равно дисперсии D, причем дисперсия стационарной соучайной функции

Z), = {t, i) = КАЩ = const. (1.185)

AHajiorH4Hoe равенство существует и для средних от произведения:

КАг)= lim -- т-«.2Т

[х(()- т,] X

X lxit+x)-mAdt. (1,186)

Фурье-изображение корреляционной фу1ищии Кд(т) стационарного случайного процесса

S,(e>)= ? (МВТ)

называется спектральной плотностью случайного процесса X{t).

Фурье-изображение функции J?v)i(t)

S«((0)=- ] R,yiT)e Чх (I.ISS)

называется взаимной спектральной п.чяп-ностью стационарных случайных процессов Х{1) и- У(().

Случайный сигнал, у которого S(a)) = = So =s const,называетсябелы.мшул1аи.Этому Фурье-изображению oiBCnaei оригинал

A.(t) = So5(t), (1.189)

(де б (т) - единичная импульсная функция, или функция Дирака, определяемая выражениями

6(т)-а при тО,

8(т) = сх) при т = О;

I S(T)rfT = 1.

(1.190)

0 1 2 3 4 5 6 7 [8] 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121