Слаботочка Книги

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 [35] 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92

мощью единственного комплексного критерия - джоулева интеграла, характеризующего количество тепла, выделяющегося при прохождении токового импульса. Его использование как главной характеристики быстродействующего предохранителя связано с тезисом о том, что количество тепла, которое выделяется в приборе, проводнике или любом защищаемом элементе, принимается равным

Ridt, где 0--длительность импульса. Однако сопротивление полупроводникового вентиля не является постоянным, а зависит от температуры, которая в свою очередь определяется током в данный момент времени. Реальная тепловая нагрузка на вентиль будет зависеть от формы импульса тока и его длительности. Поэтому фактический нагрев вентиля может быть различным при одинаковых значениях джоулева интеграла. Значит, и стойкость вентиля, определяемая его допустимым интегралом, не будет постоянной. С увеличением длительности токового импульса с 10 до 1000 мс допустимый интеграл вентиля возрастает практически линейно, поскольку при этом улучшаются условия охлаждения.

В пределах 10 мс картина получается сложной в зависимости от амплитуды, формы и длительности импульса, о чем подробно говорилось в гл. 1. В связи с этим были предприняты попытки использовать для оценки теплового действия импульса произвольной формы такие параметры, как J idt, J idt и др. Однако они не получили достаточного распространения в практике, и в настоящее время используется только джоулев интеграл, который, строго говоря, не является адекватным показателем теплового воздействия на вентиль. Следует иметь также в виду, что изготовители предохранителей обычно указывают наибольшее значение джоулева интеграла, в то время как изготовители вентилей указывают его минимальное значение, выдерживаемое вентилем и базирующееся на статистической обработке результатов испытаний.

Среди защитных характеристик предохранителя важное значение имеют преддуговой джоулев интеграл и дуговой джоулев интеграл. Ниже анализируется влияние параметров аварийного режима и характеристик предохранителя на значение джоулева дугового интеграла. Анализ базируется на предложенной авторами [2.17] методике и прямоугольной аппроксимации вольт-секундной характери-

стики дуги. Джоулев дуговой интеграл при прямоугольной вольт-секундной характеристике дуги постоянного тока имеет вид

«3

АиЧп

(4.19)

где L, i? - индуктивность и активное сопротивление контура; AU=Un~Uc; f/д - напряжение на дуге; С/с - напряжение сети; /о - ток плавления плавкого элемента предохранителя.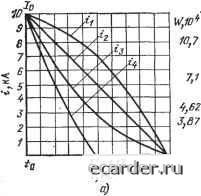

идо S)

Рис. 4.6. Изменение тока ("а) и джоулева дугового интеграла {б) предохранителя при различной форме напряжения на дуге: «=5-10-3 Ом; L=5-1C-S Гн; /„=10 кА; и =900 В; «„„=00 В; и.„.=

=900

В; i,=f(ua.i); 2=ff«„oJ; h=f(ui); Ч=Пи,)

Преобразовав это выражение с учетом Up/Uc=k, получим

(/е„1)Чп V/k + fe-l 05/0!

k - 1 /]

(4.20)

Из (4.20) очевидно, что дуговой джоулев интеграл прямо пропорционален индуктивности и постоянной времени контура КЗ и линейно зависит от напряжения сети.

Теория обосновывает, а практика подтверждает существенное влияние на дуговой интеграл амплитуды и формы напряжения на дуге даже тогда, когда среднее значение напряжения на дуге за время действия дуги оказывается одним и тем же. В качестве примера на рис. 4.6 показаны изменения тока и джоулева дугового интеграла предохранителя при различной форме напряжения на ду-

2,73s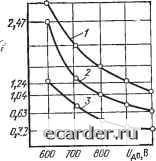

Рис. 4.7. Зависимость джоулева дугового интеграла от напряжения на дуге при различных постоянных времени контура: /о=10 кА; {/=500 В; ;-Т=10 мс: t=2X ХЮ-» Гн; R=2-1(H Ом; 2 - 1=20 мс; L= = 1-10-4 Гн; /г=5-10-3 Ом; 3=10 мс; L= =5-10-5 Гн; /г=5-1С-з Ом

ге, рассчитанные по методике, приведенной в гл. 7. На рис. 4.7 показаны зависимости джоулева интеграла от прямоугольного напряжения на дуге [/д при различных постоянных времени. Из приведенных кривых видно существенное влияние указанных факторов на значение джоулева дугового интеграла предохранителя [4.2].

Коммутация предохранителем контуров переменного тока исследована в [4.3]. Расчеты проводились в диапазоне параметров контура КЗ и предохранителя г]?-0-=-90°; cos ф=0,05-0,2; С/с=2001000 В; /к=50-=-145 кА (режим, близкий к адиабатическому нагреву); [/д=400- 1500 В; 5=0,5-1,0 мм; См=8-10" А-с/мм" (5 -сечение перешейков для предохранителей на номинальный ток 400 и 800 А; См - константа Мейера для серебра).

Влияние созф как характерного параметра цепи переменного тока эквивалентно влиянию постоянной времени % в цепи постоянного тока. Снижение cos ф вызывается увеличением индуктивности нагрузки: например при cos ф= = 0,1 полное сопротивление контура примерно на 98% определяется индуктивностью. Однако с учетом того, что абсолютное значение индуктивности в цепи переменного тока примерно на порядок меньше, чем в цепи постоянного тока, роль cos ф не столь велика, как роль т. Влияние напряжения сети и его связь с напряжением иа дуге можно оценить так же, как и для цепей постоянного тока. При этом следует использовать среднее значение напряжения на дуге за время действия дуги. Из расчетов следует, что при увеличении тока контура КЗ ток плавления растет менее интенсивно. Например, при токе контура /к= = 145 кА (/ном=400 А) ток плавления равен 10,6 кА, а при /к=14,5 кА ток плавления снижается всего лишь до 6,8 кА, т. е. ток контура изменился в 10 раз, а ток плавления лишь в 1,55 раза. Время плавления при этом изменяется сильнее (в 2,74 раза для данного примера). Таким

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 [35] 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92