|
| |
|
Слаботочка Книги Ek- В этом е-м элементе значения функции в его любой точке определяются через значения этой функции в узлах i, j, k и координаты точки с помощью полинома в ииде E-NiEi+NiEj+NkEk, (5.21) где Л;, Nf, Nh - безразмерные функции формы для каждого узла элемента. Для каждого узла данного элемента функция формы имеет шое численное .значение. Функция формы для данного узла, например функция Ni для узла i, равтаа единице, а для других узлов элемента равна нулю. Значения функций формы Ni, Nj, Nh определяются следующим образом в зависимости от координат узлов: Лг=-~-К- + М + с,г/], где ai = Xjy - ху, = у,-~Ук; Ci = x - х,. 11 Oj + bjXCiy\\, где й] = XkVi - Xiy„\ b; = - у,-; с,- = х, - х, где akXiyj - Xjyi-, b = yi - yf, = Xj - Xf (5.22)
=Xj-yi, - xyj + yjXi - yxt -f xyt - xyi, (5.23) где S - площадь треугольного элемента. Частные про1ИЭводные для искомой функции Е, где индекс е означает шринадлежность Е к данному элементу, имеют вид дЕ" дх дЕ dNi , > Е -4- Е Л-Е ~-Г flu + дх dNk £ ду ду """Г ду I ду В матричной форме выражение для Е имеет вид (5.24) (5.25) Представленные ооотношения для 1интерполяци1онного полинома и его производных составляются для всех элементов [Исследуемой области D. Получается система уравнений, количествО которых равно числу элементов. С помощью этой системы конечные элементы объединены в единое целое; интерполяционные функции для каждого элемента выражаются через глобальные узловые значения этих функций 1и глобальные координаты. Таким образом,, каждое из уравнений содержит глобалъные значения (параметры), но относится к конкретному элементу. Для нахождения .значений функции в узловых точках необходимо .значения для каждого элемента подставить в выражение для /(£), предварительно их продифференцировав, и выполнить две основные операции: заменить, интегрирование поэлементным суммированием по всей площади области D и 1ПрО!извести минимизацию этого функционала путем Приравнивания нулю его частных производных по узловым значениям. Знание значений функции в каждом узле позволяет определить ее в любой точке области с помощью интерполяционного полинома, являющегося функцией координат, и таким путем .получить пр.ибли-женное решение в виде 1куоочно-непрерывной функции. 5.2. Температурное поле плавкого элемента При расчете темпер1атур.иого пол,я плавкого элемента с помощью МКР используется такая же дискретизация области на элементарные участии, как и огаисанная выше (ом. ряс. 5.2). При этом .исходное уравнение теплопроводности (5.1) аппроксиМ1ируется конечно-разностной схемой Кранка - Николсока и решение для температуры Ti,- любого внутреннего узла, имеющего координаты i, j, в обла-ласти D в (/г+1)-й временной шаг представляется в виде = 2(achV(M0 + 2) + + + + 7.%, + Ти. / + Гн-.. / + п. у , -f п., Н-.) + аст/Ш - 2 ach/Ш + 2 п {- "ftV() f (/?,). (5.26) где р - температурный коэффициент сопротивления; fi/" -функция, представляющая локальное термическое оонрютивление и учитывающая теплоотдачу в (Наполнитель. Таким обр,азом, температура в каждом узле г, / в любой .момент времени [(п--1)-й временной шаг] определяется в завиоимости от температуры Г,-/" этого узла в предшествующий момент врем.вки, температур четырех соседних узлов в предшествующий и искомый моменты вре- Рис. 5.3. Пример разбиения температурного поля на элементы: / - прямоугольный; 2 - треугольный; 3- криволинейный; 4-узловые точки элементов; 5 - граничная поверхность с заданной температурой (Г=100°С); 6 - граничная теплоизолированная поверхность 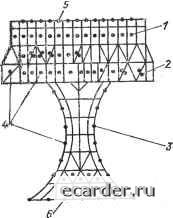 менн С учетом .плотности тока, удельного электрического сопротивления и теплоотдачи в нанолкитель в тредшест-вующий момент времени. Ур.авнения такого типа составляются для каждого .вн.утр1еннего узла области D. Для определения решения ,на каждом временном шаге решается система алгебраических уравнений. Выше при использовании МКР конечно-разностное у.рав.нение получали из дифференциальвого уравнения теплопроводности. В некоторых случаях исходят непосредственно из уравнения теплового баланса, отражающего законы оохр.аНения энергии, Фурье и Ньютона для отдельного элемента. В этом случае применяется проце-дура, включающая в .себя разбиение И100Ледуем.ого температурного по.ля на элементы (элементарные участки), составление уравнений теплового .баланса для каждого элемента, вывод уравнений в конечных разностях и численный расчет на ЭВМ. На рис. 5.3 сложное температурное поле разбито на прямоугольные, треугольные и криволинейные элементы. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 [50] 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 |