Слаботочка Книги

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 [54] 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92

ния жесткости плавкого элемента. Представляется целесообразным решить поставленную задачу с помощькз» изменения пространственной формы (изгиба) плавкого элемента. ВВИду 1СЛ10ЖНОСТИ теюретичеснопо анализа жесткости ленточного произвольно изогнутого элемента введем следующие допущения: 1. Усилия растяжения-сжатия F,. обусловленные температурными напряжениями, действуют только IB местах .расположения параллельно соединенных;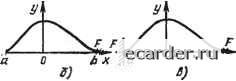

6 К:

Рис. 5.7. К расчету жесткости плавкого элемента:

а-эскиз произвольно изогнутого плавкого элемента: ПП-плавкие перешейки,, в сечении которых действует сила F; б - эквивалентный стержень с двумя подвижными точками а и 6, в которых действует сила Fi в - эквивалеитиая стержень с неподвижно закрепленной точкой а и подвижной точ-сй *

перешейков, которые равномерно распределены по ширине плавкого элемента и являются наиболее нагретыми его участ:кам,в (piHc. 5.7,а).

2. Приняв равномериое распределение усилий но ширине элемента, рассматриваем одиночный стержень, (рис. 5.7,6), полученный разрезанием ленточного элемента на параллельные иити (стержни) и имеющий В1ид; кривой y-f{x).

3. Усвлия F действуют непосредственно у точек а т b этой кривой, что соответствует расположению перешейков на плоской части плавкого элемента в непосредственной близости ОТ места перегиба. В точках а io. b пр1ил1оже-иы две Одинаковые (и противоположно Направленные юи-лы, под действием которых оба ионца стержня; перемещаются.

Для удобства анализа заменим систему сил одной-силой F в точке 6 при жестком закреплении конца а. Новая система полностью эквивалентна предыдущей -по равнодействующим Силам, .так как в точке а действует реакция, однако теперь перемещается лишь конец Ь. Перемещение этого конца определим с помощью интеграла-Мора, представляющего собой группу из шести интегральных выражений, лолученную на основе теоремы Ка-стильано для перемещений точюи мод действием нескольких сил. В расоматриваемом случае основную ролъ иг-

рают лишь изгабные перемещения точки b в- вертикальной плОСкости; перемещения вследствие растяжения и сдвига будем считать .пренебреж1и,мо малыми. В Связ;и с этим достаточно ограничиться одним криволинейным интегралом Мора .первого рода, определяющим перемещение бь ТОЧ1ИИ Ь .из-за изгиба:

S,=JiWL, (5.35)

где M\=Fy{x) - МОмент суммы всех сил, действующих ,на стержень; в данном случае это одна сила - реакция F опоры; Мр=.Ру{х)-момент силы в точке перемещения Ь; dl - элемент дуги стержня, выраженный в декартовых координатах и равный У1+[у{х)]Чх; J=d№/\2 - момент инерции прямоугольного сечения стержня относительно центральной оои; d - ширина стержня; h - толщина стержня. Подставив значения этих параметров 1в интеграл Mopia, получим

() yy+WV. (5.36)

Найденное таким образом перемещение Ьь точки Ь кр.ивой y=f{x) позволяет оиределить в самом общем ви> де жесткость произвольно и.зогнутого стержня как отно-апение Силы к перемещению:

G = EJ ~-\-. (5.37)

Часто более удобным может оказаться аНаяиз в полярной Системе координат, в которой параметры ироиэволь-ной точки хар-актеризуются радиусом-вектором р и углом <р (рис. 5.8,с). В силу справедливости интеграл1а Мора 1и соотношений

Afi=Mp=psin(p; dl=pdq) (5.38)

выражение для перемещения .принимает вид

= -~ о sitf cpcfcp. (5.39)

Значения начального и конечного углов фн и фк равньв соотоетспвенно О и jt, так что формула для расчета жесткости стержня в полярной системе координат иред-ставлзетоя следующим образом:

(5.40>

В качестве примера определим жесткость стержня, изогнутого прямоугольником ABDE (рис. 5.8,г). Ввиду сим-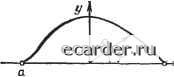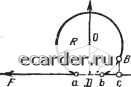

1/2 1/2

а J] Ь

£ F

Рис. 5.8. К расчету жесткости плавкого элемента в полярной системе

координат:

а - эквивалентный произвольно изогнутый стержень; б - стержень, изогнутый »• виде полукольца; в - стержень, изогнутый в виде кольца; г - стержень, изoгнy: тый в виде прямоугольника

метрши системы будем анализирювапъ участок ABC, который разобьем на две части - АВ и ВС. Дли каждой из, них найдем моменты и элементы дуги и затем перейдем к интегралу Мора. Выберем произвольную точку N на участке АВ, положение которой характеризуется радиусом-вектором р 1И углом ф. Введем обозначения

AO=OE=R; AB=OC=ED=H. Для участка АВ

(5.41>

9„ = arctg ; = Ж = tg 9 = /? tg 9, (5.42>

cos у

cos2 If

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 [54] 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92