|
| |
|
Слаботочка Книги мировании обобщенного критерия методом субъективного и формального объединения частных критериев, подобным, описанным выше, и весьма редко учитывали физическую суть исследуемого явления и объективно существующие соотношения между частными критериями. Если такого, рода обобщенный критерий - вектор X=f(Xi) найден тем или иным путем, то при наличии одного ограничения b{Xi)C (i==l, 2, ... , n) оптимальные значения Xiopt (i=l, 2, п), доставляющие максимум Хтах обобщенному критерию, могут быть найдены методом неопределенных множителей Лагранжа. С этой целью вначале образуют вспомогательную функцию F(xi)=f(xi)+X[b{xi)-C], где X - неопределенный множитель. Затем приравнивают нулю все частные производные этой функции по критериям Xi (у. \ df{, Xg,Хп) , дх,. - • "> ~ дх,- + -4-я Ь{Х:,,Х„...,Хп) . 2,... , п. в результате получают п уравнений вышеприведенного типа с (n-fl) неизвестными Xi, Х2, ... , Хп, К. В сочетании с ограничениями b(Xi)C формируется система (п-Ы) уравнений. Совместное решение уравнений этой системы позволяет найти оптимальные значения частных критериев . Xiopt, X2opt, ... , Хп opt, доставляющие максимум обобщен- ного критерия Xmax=f{Xiopt, Xzopt, Хп opt) Если для задачи действует не одно, а два или более ограничений вида b{xi)C, то эти ограничения вводятся как слагаемые в приведенное выше уравнение для F(Xi). Каждое слагаемое вводится со своим неопределенным множителем, после чего задача решается по такой же схеме. Следует отметить, что если первый из упомянутых приемов формирования обобщенного критерия характеризуется субъективностью,, то второй - чрезвычайной сложностью реализации. Стремление к объективности и упрощению решения задачи многокритериальной оптимизации привело к появлению в начале 70-х годов подхода, основанного-на использовании теории аналитических игр и получившего название «шринцип оптимальности по Парето». Этот метод представляется единственным в настоящее время формально-математическим методом решения задач векторной оптимизации. В отечественной экономической литературе (работы Л. Н. Волгина) он называется принципом согла- сованного максимума. Оптимальность по Парето или неподчиненность предполагает оптимальным такое решение, при котором любое улуч- .шение одной целевой функции (одной составляющей вектора многокритериальной оптимизации) может быть достигнуто лишь за счет ухудшения другой. Этот принцип впервые описан применительно к аналитической теории игр в 1909 г. Первые попытки технических приложений лринципа Парето в США и Японии были предприняты лишь в середине 70-х годов. Одним из необходимых условий оптимизации по Парето некоторой -функции f{x) при ограничении bi(x)0 {i=l, 2,..., п) для некоторой области R служит теорема Куна - Такера, которая формулируется следующим образом. Если f(x) и hi дифференцируемы в точке х* и если для любого Z удовлетворяется условие Z{dbt{x*)ldx)0 при -Любых 1, причем bi(x*)=Ot и z направлено из точки х* в R, то необ-:ХОДИмым условием того, чтобы X* была локальным минимумом в рассматриваемой задаче, является существование таких %i*(i=l, 2,...,п), что bi{x*)0; %i4t(x*)=0, Х.-*0; где X* - множители Лагранжа. Если f(x) и bi(x) являются выпуклыми функциями, то условия, задаваемые теоремой Куна - Такера, будут как необходимыми, так и .достаточными. В случае рассмотрения двух целевых функций fi{xi, х) и f2(xi, Х2), -зависящих от двух параметров, оптимальные по Парето значения этих .параметров должны удовлетворять условию dxi дх dx+dxO. dXj дх2 Это однородная система двух линейных уравнений относительно полных дифференциалов dxi и dx2, имеющая, как известно, нетри-.виальное решение, если ее определитель равен нулю «и «21 = 0, Тдеа,-/=-(i, / = 1, 2)-частные производные (или векторы-гра- лиенты целевых функций). Условия оптимальности по Парето означают параллельность векторов-градиентов целевых функций и их противоположную направленность, что позволяет представить вышеприведенное соотношение с помощью вспомогательного параметра К в виде 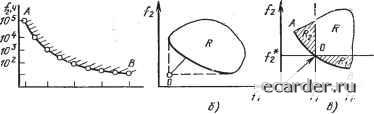 "wo 500 600 700 800 f,,A/MM а) Рис 511. Оптимальность по Парето- Эти соотношения в неявном виде описывают компромиссную кривую, на которой расположено множество оптимальных по Парето точек. Дополнительные ограничения; типа b{xi, Х2)=С позволяют разработчику найти на этой кривой точку оптимальности xi*, Х2*. Пример компромиссной кривой для двух целевых функций fi - плотности но минального тока в перешейках быстродействующего предохранителя и f2 - стойкости предохранителя к воздействию циклически изменяющейся токовой нагрузки (в часах) приведен на рис. 5.11,а. Компромиссная кривая проходит через точки А и В абсолютных оптимумов для каждой целевой функции, определяемые условиями ai = dfi/dx=d; 02=/2/ = 0; х={хи Х2); ai=>ia2. На отрезке компромиссной кривой между точками абсолютных оптимумов обеих целевых функций положительному приращению одной из функций соответствует отрицательное приращение второй функции, т. е. вспомогательный параметр К на этом отрезке является отрицательной величиной. Переход от точки абсолютного оптимума одной целевой функции к аналогичной точке второй целевой функции соответствует изменению К от О до -оо. Компромиссная кривая содержит все возможные-оптимальные решения и конкретная точка оптимальности находится, как уже отмечалось, с использованием ограничений. В некоторых случаях (например, при неизвестных ограничениях) целесообразен иной подход, при" котором из мно- 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 [62] 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 |