
 | |
|
Слаботочка Книги 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 [19] 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 https://kuznetsov.studio Разработка сайтов Ростов-на-Дону. Kostj студия Разработки. 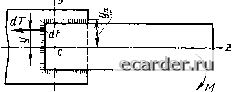 Рис. 2.39. Сварное соединение в плоскости изгибающего момента М. Расчет швов по осевому моменту инерции Так как в зоне о напряжение Tq = О, то проверки результирующих напряжений не требуется. Определим напряжения в том же соединении методом расчленения на два горизонтальных шва и один вертикальный по формуле (2.47): т = 0,025/(0,7-0,01 -0,1 (0.3+0,01)-f 0,7-0,01 • 0,32/6) = 77,6 МПа. По этому способу расчета т постоянно по длине горизонтальных швов. Расчетное результирующее напряжение в пересечении горизонтального и вертикального швов (рис. 2.38, в) равно т:рез = /77,62+11,92 = 78,5 МПа. Расчет прочности по способу полярного момента инерции дает большее значение напряжения, поэтому вычисление напряжения по этому способу обеспечи-§ вает больший запас проч- ности. В основе расчета по способу осевого момента инерции лежит допущение, что напряжения в швах пропорциональны деформациям в основном металле (рис. 2.39) и, следовательно, возрастают в линейной зависимости от расстояния точки до нейтральной оси элемента. Реактивное усилие в элементе равно dr = Tdf. (2.55) Реактивный момент в элементе определяется по формуле dM = dr. (2.56) Полный момент внутренних сил M==\ydT=rydF. (2.57) Принимаем, что напряжения представляют собой линейную функцию расстояния до оси. При этом т/т1 = г 1, где Tj - напряжение на расстоянии, равном единице от оси г. Тогда М = Хг\уйР. (2.58) Интеграл выражает момент инерции швов относительно оси г. Наибольшее напряжение -max - M/(I,y,,}[r]. (2.59) Результаты расчета прочности по способу осевого момента незначительно отличаются от результатов расчета по способу расчленения соединения на составляющие. Наиболее часто применяют первый способ, особенно при конструировании соединений с учетом заданных усилий. Второй способ используют для опредмения расчетных напряжений при заданных размерах соединений. Третий способ используют в тех случаях, когда расчленение соединений затруднительно. При рассмотрении прочности прикреплений элементов, работающих на изгиб, будем предполагать, что угловые швы имеют форму равнобедренного треугольника. Расчет прочности производится на срез в плоскости, совпадающей с биссектрисой прямого угла и равной по площади р/Са, где К - катет шва, а - длина шва. Определим напряжения в сварном соединении, прикрепляющем балку прямоугольного поперечного сечения, работающую на изгиб, относительно оси x- x (рис. 2:40, а). Соединение сконструировано с угловыми швами, охватывающими профиль по периметру. Нормальные напряжения в балке вызывают касательные напряжения т в швах: -[т]. (2.60) 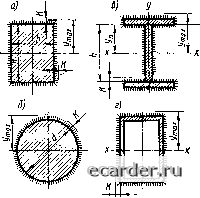 Момент сопротивления lJ7c=/c/l/max. (2.61) Рис. 2.40. Сварные соединения элементов, обваренных по периметрам угловыми швами: а - прямоугольное сечение; б - круглое сечение; в - двутавровое сечение; г - коробчатое сечение где /(. - расчетный момент инерции периметра швов относительно оси x - х.С учетом возможного разрушения по наименьшему сечению /с = /р, где / - момент инерции периметра швов, т. е. /, = р {2/Cb[(/i + K)/2p + 2/C«b/12 + 2/C(/i + 2K)/12}; (2.62) (/max =/1/2 +/С. (2.63) Для круглого поперечного сечения (рис. 2.40, б) /, = Р[я(с/ + 2/С)*/64-яй*/64]; (2.64) (/max = d/2 + K. (2.65) Расчет прочности прикрепления произвольных профилей двутавровых, коробчатых (рис. 2.40, в, г), тавровых и других производится так же, как в случаях, рассмотренных выше, на основе формул (2.60) и (2.61). Если элемент работает при сложном сопротивлении - изгибающем моменте М и продольной силе N, то суммарное напряжение в соединении равно Т = ~1/шах+, (2.66) где - расчетная площадь швов: F.KL, (2.67) где L - длина периметра швов. Если элементы нагружены поперечными нагрузками, то в них возникают изгибающие моменты М и поперечные силы Q. Напряжения в сварных швах от действия силы Q определяют с учётом следующих допущений поперечная сила воспринимается только вертикальными швами, распределение напряжений по длине вертикальных швов равномерно. Таким образом, среднее напряжение в шве от поперечной силы равно ro = Q/F„ (2.68) где F„ - расчетная площадь вертикальных швов. На уровне верхней кромки вертикального листа в швах следует проверить результирующие напряжения от действия момента и поперечной силы. Напряжение от момента (2.69) где Уа - расстояние от оси, проходящей через центр тяжести сечения, до горизонтальной верхней кромки (рис. 2.40, в). Напряжение от поперечной силы Xo = Q/(2p/C/j). Результирующее напряжение Трсз = к + Ti [Т]. (2.70) (2.71) Практика расчетов показывает, что проверка прочности по формуле (2.60) является решающей. Вид А .180x6 Н=Вмм 1 = 100 см Р=50НН Q=25HH 190мм Рис. 2 41. Расчет швов соединений при сложном сопротивлении Пример расчета. Консольная балка двутаврового профиля (рис 2 41) прикреплена по периметру угловыми швами с катетом /С = 6 мм, продольная сила Л" = 50 кН, поперечная сила Q = 2,5 кН, сварка полуавтоматическая (Р = 0,8). 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 [19] 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 |