Слаботочка Книги

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 [27] 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89

Коэффициент концентрации напряжений в паяном шве

«о = ?тах/7о = аЯ/ [(1 + ch a/)/(sh al)]/2P = а/ [(1 -f ch a/)/<ah a/)]/2.

(2.110)

Коэффициент a<j определяют в значениях функции от 2Gs/{FS(j) (рис. 2.64). Чем меньше отношение G/E, тем соответственно меньше коэффициент концентрации.

Преимуществом паяных швов является возможность образования пластических деформаций в нахлесточных паяных соединениях, сопровождаемых снижением напряжений в крайних точках соединений и выравниванием эпюры напряжений по длине соединения.

При сопоставлении значений концентраций напряжений в паяном и сварном нахлесточных соединениях, состоящих из двух лобовых швов, коэффициенты концентрации напряжений высоки в обоих случаях, но при пайке они ниже. Это обстоятельство объясняется более рациональной конструктивной формой паяного соединения по сравнению со сварным.

ГЛАВА 3

МЕХАНИЧЕСКИЕ СВОЙСТВА СВАРНЫХ СОЕДИНЕНИЙ § 1. Некоторые понятия теории упругости и пластичности

Определение некоторых механических свойств металлов производят, используя простые схемы нагружения - растяжение, сжатие, кручение. При растяжении получают диаграмму зависимости условных напряжений а = P/Fq от условных деформаций 8 = А /о, используя силу Р, первоначальную площадь поперечного сечения F, удлинение образца А/ и первоначальную расчетную длину образца Ig. Условная диаграмма зависимости напряжений от деформаций (рис. 3.1) позволяет определить предел пропорциональности - тОЧКа А; действительный предел текучести, при котором начинаются пластические деформации, - точка В; условный предел текучести Оо,2 - точка С как пересечение пршж)р линии, которая параллельна упругому участку диаграммы OA и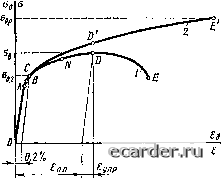

Рис. 3 1 Диаграмма растяжения металла: / - условная, 2 - действительная

отсекает на оси е отрезок величиной 0,2 %, с кривой линией Диаграммы; временное сопротивление Од - точка D, при котором наступает потеря пластической устойчивости и начинает появляться шейка; напряжение разрушения металла- точка Е. Измерением длины 4 и диаметра шейки разрушенного образца определяют также относительное удлинение б = (4 - /о) о и поперечное сужение jj) = (Fo - Ек)/Ро, где Ек - площадь минимального сечения шейки образца после разрыва.

Диаграмму условных напряжений используют для построения диаграммы действительных напряжений Од и деформаций Ед. Д е й-ствительные напряжения находят как отношение силы Р к действительной площади поперечного сечения образца Од = P/F, а действительные деформации - как интеграл бесконечно малых приращений относительных деформаций dl/t:

бд 5d / = ln( /o) = In[(/o + A/) o] = ln(l+e). (3.1)

Действительные деформации 8д, или, как их еще называют, логарифмические, заметно отличаются от условных деформаций е, если значения последних превышают 0,15-0,2 (15-20 %).

Полная деформация состоит из упругой и пластической:

e = 8y + F„,. (3.2)

Коэффициент поперечной деформации (коэффициент Пуассона) в пределах упругих деформаций

= -е.гоп/еу-0,25-f-0,3. (3.3)

За пределами упругости приращение продольных пластических деформаций вызывает поперечную деформацию с коэффициентом 0,5, в то время как приращение упругих деформаций продолжает вызывать поперечные деформации с прежним коэффициентом fiy. Поэтому коэффициент Пуассона, обозначенный за пределами упругости как ц, изменяется по мере роста пластической деформации от [1у до 0,5:

= - е„оп/е = - [Uy (e/e) -f 0,5 (8„,/б)]. (3.4)

Так как пластическая составляющая деформации имеет коэффициент поперечной деформации ц„„ - 0,5, то это означает, что изменения объема от пластических составляющих деформации не происходит.

Закон неизменяемости объема при пластической деформации может быть записан как

чх +Чу +ег =0, (3.5)

пл "пл пл

где , , - действительные пластические деформаций

ПЛ пл Okfl

в направлении координатных осей х, у, г. Упругие составляющие деформации вызывают изменение объема тела.

При неодноосном напряженном состоянии в общем случав в каждой точке тела имеются напряжения а, Оу, о, Тху, туг, zx и деформации e,, е,, е, уу, Ууг, Угх- Важными характеристиками напряженного и деформированного состояния являются оун*-интенсивность напряжений, е, - интенсивность деформаций:

Oi = {\lY~2) V{Ox - Oyf -f {Оу - -f (a, - Oxf -f 6{%ly -f %1г -f tL);

(3.6)

Щ = (К2/З) Y(8., - ByY + (8 - e,) + (8, - 8.,) +

+ m{yly + ylz + ylx) (3.7)

В случае выбора главных осей

at = (I/K2) V{oi - of -f (da - of + ((Тз - o,f\ (3.8)

8, = (К2/З) У (8i - 82) -f (82 - 63) -f (63 - Hyf. (3.9)

Энергетическая теория пластичности принимает, что пластические деформации при сложнонапряженном состоянии возникают при а,- = От (от -предел текучести). Это положение в целом хорошо подтверждается экспериментами. Из него, в частности, вытекают некоторые важные в практическом отношении следствия. При трехосном растяжении или сжатии отдельные компоненты могут заметно превосходить предел текучести металла, но при этом Oj <; От и пластические деформации не возникнут. При двухосном напряженном состоянии, когда = -о, а Og = О, что соответствует чистому сдвигу, пластические деформации начнутся при максимальном напряжении = а/З < а,.

Для расчетов напряженного состояния за пределами упругих деформаций используют теории пластичности. Одно из основных положений теорий пластичности состоит в том,что для различных напряженных состояний конкретного металла принимается справедливой одна и та же экспериментальная зависимость между напряжениями и деформациями.

Деформационная теория пластичности устанавливает единую связь между интенсивностью напряжений а,- и интенсивностью деформаций 8,- независимо от схемы напряженного состояния. Эта связь может быть найдена для каждого конкретного металла из результатов испытаний на одноосное растяжение. При этом напряженном состоянии согласно (3.8) получаем 0{ = о. Связь между и 8 найдем с учетом = 8 и зависимости (3.4), из которой полегчаем 82 = 83 = -це. Тогда согласно формуле (3.9) имеем

8; = (2/3) (1 -f .а) е = е - Ео = Б - (1 - 2[iy„) а/{ЗЕ), (3.10)

где 8о = (8 -Ь 62 -Ь ез)/3 - средняя деформация, которая связана со средним напряжением Од = (oi + 02 + a<,)/3 зависимостью 8о = = (1 - 2fiynp) Оо/Е. Так как 02 = 03 = О, то Оо = oJS = о/З.

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 [27] 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89