Слаботочка Книги

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 [37] 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89

a<j примерно совпадает скоэффициеитом концентрации деформаций

«в = в.,зх/Чр. (3.30)

Коэффициенты концентрации напряжений a<j и деформаций ag в упругой области не зависят от уровня приложенных напряжений Ох.

Если максимальное напряжение достигнет предела текучести 0т, вблизи концентраторов появятся зоны пластических деформаций. Коэффициент концентрации напряжений a<j по мере роста нагрузки будет уменьшаться вследствие отставания роста 0» от Ох (рис. 3.30, в).

Если t, то изменение h при постоянном t мало влияет на коэффициент концентрации напряжений. Такие надрезы называют мелкими. Коэффициент концентрации в них зависит от изменения t. Чем больше t, тем выше коэффициент концентрации. Наоборот, при th коэффициент концентрации напряжений в основном зависит от изменения h и мало зависит от изменения t. Такие надрезы называют глубокими. В них чем больше h, тем выше коэффициент концентрации напряжений.

Чем меньше радиус концентратора р и угол а между его плоскостями, тем выше коэффициент концентрации. При а = О, когда грани параллельны, коэффициент концентрации a<j~") /p или a<j Vhl р.

В последние два десятилетия для оценки прочности металлов при наличии в них трещин применяют положения линейной механики разрушения. Она оперирует с концентраторами, у которых р = 0. В этом случае расчетное механическое напряжение становится равным бесконечности, а понятие коэффициента концентрации напряжений теряет свой смысл. Для оценки поля напряжений вблизи концентратора используют понятие коэффициента интенсивности напряжений в вершине трещины при упругих деформациях, обозначаемого К, и понятие интенсивности освобождения эиёргии деформации, обозначаемой G. Рассмотрим растянутую напряжениями о тонкую бесконечную пластину (плоское напряженное состояние), имеющую разрез в виде трещины а == О (рис. 3.31, а), и в виде выреза с а О (рис. 3.31, б).

Для трещины длиной / в бесконечной пластине формула коэффициента интенсивности напряжений имеет вид

К = УТЩоУ1; (3.31)

а для интенсивности освобождения энергии

G=no4/(2E). (3.32)

Величина К характеризует распределение напряжений у конца трещины и выражается в Н/м"/», а величина G- это энергия, освобождающаяся в растянутой пластине при возможном подрастании

трещины на единицу площади; ее единица - Дж/м Обе эти величины взаимосвязаны: в случае плоского напряженного состояния

G = KIE; (3.33)

при плоской деформации

G{\-p?)K4E. (3.34)

Понятия плоского напряженного состояния и плоской деформации даны в § 1.

Для других случаев расположения трещин, например в растянутой полосе, при боковых трещинах глубиной t (см. рис. 3.30, а), значение К зависит от отношения размеров tlh. При th К rYh и практически не зависит от t. Аналогичным образом К зависит от линейных размеров и при изгибе образцов. При изгибе К также пропорционален а, которое берется без учета концентрации напряжений. Например, а =

= 0„ = MIW

(рис.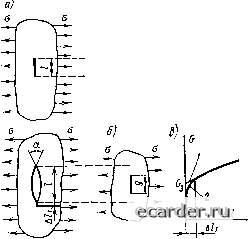

Рис. 3.31. Бесконечная пластина с надрезами (Р = 0):

а - трещина с а == 0; б - вырез z а.ф 0; в - изменение а

3.32, а), где W = sh/6, S--толщина пластины. В ряде случаев в формулах для вычисления К используют среднее напряжение без учета ослабления, т. е. W = = SBV6, а = P/F (рис. 3.32, б), где F = Bs~ площадь поперечного сечения.

Величины К G используются для оценки свойств металла при наличии в них трещин.

При испытании в момент начала движения трещины регистрируют уровень критического напряжения о и, зная размеры образца и трещины, вычисляют по соответствующим формулам критические значения Кс и G для испытуемого металла (подробнее эти вопросы освещены в следующем параграфе).

Для надрезов, заканчивающихся, как и трещина, нулевым радиусом, но имеющих угол а =7 О (рис. 3.31, б), значение и размерность К зависят от угла а. Если в острие такого выреза есть небольшая трещина A/i (рис. 3.31, б), значения величин К G, имеющих в этом случае уже обычные для себя единицы Н/м/ и Дж/м, зависят не только от А /, но и от длины выреза / и угла а, причем рост G в зависимости от А/ происходит по закону, выражаемому кривой 2 (рис. 3.31, в), крайне быстро и значение G приближается к прямой /,

описывающей зависимость G в случае наличия трещины длиной /. При А/5э A/j кривая 2 и прямая / сливаются, что позволяет рассматривать вырез длиной I как некоторую эквивалентную ему тре-

а) М

							1 J

Рис. 3.32. Распределение напряжений в пластинах с различными концентраторами:

а - боковой надрез, афО, б - центральная трещина, в - нецентральная

трещина

щину длиной g при том же напряжении а. Размер эквивалентной трещины вычисляется по формуле

g = 2G,El{Ka\ (3.35)

где Gj, находят по рис. 3.31, в при экстраполяции прямолинейного

участка кривой 2 до пере-

сечения с осью G.

Сравнение концентраторов с острыми надрезами (р 0) между собой по длине g позволяет расположить их в определенный ряд по степени опасности, как это делают, используя понятие коэффициента концентрации напряжений a<j.

В качестве характеристики напряженно-деформированного состояния используют также понятие раскрытия вершины концентратора S. Первоначально оно было применено к концентраторам с РтО и означало приращение размера а у дна выреза (рис. 3.33, а), выражаемое как разность длин АВ после нагружения и АВ до нагружения:

ЬАВ-АВ. (3.36)

Затем это понятие было перенесено на трещины и стало означать либо раскрытие дна трещины (рис. 3.33, б), что довольно неопре-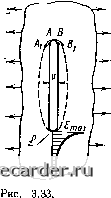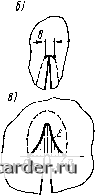

Различные случаи раскрытия б:

определения

а - изменения расстояния между точками А и В; б -раскрытие конца трещины; в - интеграл уп-ругопластических деформаций

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 [37] 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89