
 | |
|
Слаботочка Книги 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 [87] 88 89 Так как каждое соединение 1 я2 выполняется независимо от другого в одинаковых условиях, то прочность каждого сварного соединения является независимой Ьеличииой и в данном случае = Яз, а Яд: = Н\. Для определения закона распределения прочности системы /2 (Р) по известному закону распределения плотности вероятности прочности одного звена /1(Р) (одного сварного соединения) воспользуемся положением, согласно которому плотность вероятности 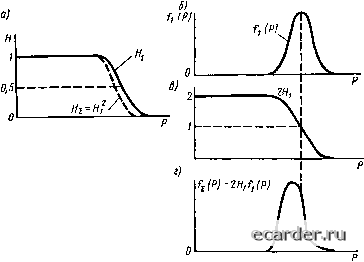 Рис. 11.7. К примеру вычисления /2 (Р) с двумя звеньями по известному Д (Р) одного звена распределения прочности равна первой производной вероятности неразрушимости. Тогда dH dm dH, h{P)-- = - = -2Hi = 2H,h{P). (11.11) На рис. 11.7, в показана кривая 2Hi, а на рис. 11.7, г- кривая fx (Р) в виде произведения 2HJi (Р). Если Принять (Р) в виде симметричной кривой нормального распределения, то функция /s (Р) является асимметричной кривой, максимум которой смещен в область меньших значений Р. Средний уровень прочности системы из двух звеньев уменьшается по сравнению с уровнем прочности одного звена. Прочность элемента определяется свойствами металла и сечением элемента. Например, прочность соединения встык на рис. 11.6,6 Р = (ГзР. (11.12) где Ов-предел прочности; F- площадь поперечного сечения. Каждая из величин о и Р имеет рассеяние. Рассмотрим изменение Р в зависимости от изменения и F. Среднее значение Р = OgP и, казалось бы, рассеяние величин о и Р не должны влиять на вероятность разрушимости. Однако дисперсия произ- ведения двух величин х а у, определ?ек)1ая по формуле D,= DxDy + xDy + gm.x, (ПАЗ) влияет на вероятность разрушимости при неизменном уровне эксплуатационной нагрузки. Пусть Ов = 500 МПа; f = 100 мм, средние квадратическйе отклонения Sa = 30 МПа, Sf = 6 мм. Соответственно дисперсии D„ = 900, Dp = 36. Дисперсию прочности найдем по формуле (11.13) Dp = 1,8-10 №, среднее квадратическое отклонение Sp = KD = 4250 Н; Р = 0вР = 5-10* Н. Коэффициент вариации силы Vp = Sp/P = 0,Ш5, 4tu заметно выше коэффициентов вариации = Vf = 0,06. f(Pl
fipl Рис. 11.8. Изменение кривой распределения и вероятности разрушимости прн фиксированном значении Рис. 11.9. Характер изменения кривой рассеяния при понижении прочности вследствие влияния концентрации напряжений Влияние среднего квадратического отклонения при неизменном среднем Р на вероятность разрушимости Ф можно видеть из примера на рис. 11.8. Разрушение наступит при Р Р, где Р - максимальная эксплуатационная нагрузка. Увеличение рассеяния при переходе от закона распределения плотности вероятности, показанного сплошной кривой, к закону, показанному пунктирной кривой, при постоянном Р приводит к росту вероятности разрушимости Фа по сравнению с Фх, которые пропорциональны заштрихованным площадкам: Ф=5/(Р)(!Р. (11.14) Конечно, площади поперечных сечений не могут настолько изменяться, чтобы существенно влиять на уровень вероятной разрушимости. Однако коэффициенты концентрации напряжений а могут оказать чрезвычайно сильное влияние. Как следует из рис. И .1, а, при малых значениях а концентраторы не влияют на прочность, но начиная с определенного уровня снижают ее примерно по гиперболическому закону P = aFla, (11.15) Это означает, что если уровень концентрации напряжений ограничен определенным значением а, то кривая / распределения прочности (рис. 11.9) не будет пересекаться с уровнем максимальной эксплуатационной нагрузки Р. Возрастание а выше некоторого определенного уровня, не изменяя существенно средней величины Рг, сильно увеличивает область левой ветви кривой 2. Заштри.хо-ванная площадь пропорциональна вероятности разрушения. Максимальные нагрузки Ртах в большинстве случаев не остаются постоянными, а могут изменяться в некоторых пределах. В этом случае, как показано на рис. 11.10, величина Ртах имеет рассеяние. Отношение средней разрушающей нагрузки Рр к средней максимальной нагрузке Ртах является в обычном понимании коэффициентом запаса. Однако может существовать некоторая 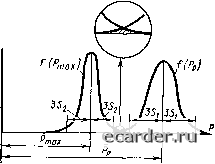 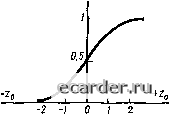 Рис. 11.10. Кривые рассеяния максимальной эксплуатационной нагрузки Ртах и прочности Рр Рис. 11.11. График зависимости Ф(гв) область, которая перекрывается двумя кривыми, что означает Ртах > Рр (на рис. 11.10 заштриховзна). Вероятность разруши- мости для этого случая будет равна J F (Ртах) / (Рр) dPmax. а в случае закона нормального распределения F (Ртах) и / (Рр) вероятность разрушения может быть вычислена как интеграл вероятности Ф (2о) по формуле (11.6), где Zq = (Ртах-Pp)/K5f + S; здесь Si и s.2- средние квадратические отклонения. Значение Zq тем меньше, чем больше средние квадратические отклонения Si и Sg, а это означает, что вероятность разрушения Ф (Zo) при неизменных средних Ртах И Рр буДСТ ВОЗраСТЗТЬ с увеличением рассеяния Ртах и Pp. График зависимости Ф (Zq) от Zq показан на рис. 11.11. В качестве коэффициента запаса при вероятностном методе оценки прочности предлагается брать п = (Рр-3Si)/(Pmax + 3Sg) (рис. 11.11). Вероятностные методы в расчетах на прочность находят все большее применение для оценки надежности деталей и конструкций. Надежность - это свойство изделия вьтолнять задан- 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 [87] 88 89 |