Слаботочка Книги

0 1 2 3 4 5 6 7 8 9 10 [11] 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119

геометрии диафрагм (круглого отверстия, узкой щели, периодического чередования этих элементов в виде решеток и т. п.) удается получить математически простые модели. Их основу составляют формулы, определяющие направления, в которых наблюдаются максимумы и минимумы интенсивности дифракционных картин. В общем виде

ф = ф(т, ХМ), (1.56)

где фгп - угол наблюдения экстремума дифракции т-го порядка (отсчитывается от направления падающего луча), т=0, ±1, ±2,..., Л- характеристический геометрический размер диафрагмы (радиус круглого отверстия, ширина щели, шаг решетки и т. п.). В случае двух- или трехмерных объектов дифракции вместо т (в 1.56) входят целочисленные аргументы т, i или т, i, j.

Два практически интересных случая - дифракция плоской волны на диафрагмах, представляющих собой круглое отверстие и две параллельные щели, - иллюстрируются рис. 1.11. Дифракция Фраунгофера на трехмерной периодической решетке приводит к известному условию Вульфа - Брэгга:

5тф„ = тА/(2й), (1.57)

где d - расстояние между соседними сетчатыми плоскостями.

Если данные рис. 1.11 использовать при рассмотрении отверстий, штрихов и включений произвольного вида, то можно сделать ряд практически важных выводов.

Дифракционная угловая расходимость параллельного пучка световых лучей

ФдиФФ = 2фо = рХ/Л, (1.58)

1 t

Sin f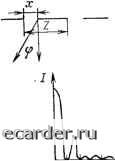

sin <р

~R R~ TLX X

a) 6)

Рис. 1.11. Дифракция на круглом отверстии (а) и на двух параллельных щелях (б)

где р=0,3... 0,6; фо определяется либо по положению первого минимума на рис. 1.9,а (p?t;0,6), либо по полуширине первого максимума (3?sjO,3).

Предельная линейная разрешающая способность оптических приборов (дифракционный предел) не может быть лучше

2„ин = 2. (1.58а)

Это следует из рис. 1.11,6, где при Z=%I2 первый максимум занимает угловое пространство фо=-л/2...-}-л/2, т. е. при любом угле наблюдения будет видна сплошная светлая полоса - обе щели сольются.

Из рис. 1.11, а также из (1.57) следуе--, что дифракция в веществе не будет иметь места, если линейные размеры вкраплений не превышают К/2; в этом случае вещество оптически однородно.

Сказанное здесь о дифракционной расходимости светового пучка, дифракционном пределе оптических приборов, о понятии оптической однородности среды носит фундаментальный характер и может претерпеть изменения лишь тогда, когда нарушаются уравнения Максвелла (например, при существенности нелинейных оптических эффектов - см. гл. 3).

При выводе математических соотношений этого параграфа предполагалось постоянство во времени всех параметров взаимодействующих волн (волн El и е2 при рассмотрении интерференции, первичной и вторичной волн при анализе дифракции). Иными словами, амплитуда, частота колебаний, начальная фаза, направление вектора поляризации оставались неизменными во времени. Такие колебательные процессы называются когерентными. Качественно понятие «когерентность» является синонимом понятий «согласованность», «корреляция» в применении к волновым или колебательным процессам.

В более общем смысле два колебательных процесса когерентны, если между соответствующими характеристическими параметрами этих процессов имеется корреляция; электромагнитное поле когерентно, если имеется корреляция между его параметрами, рассматриваемыми в разных точках пространства в разные моменты времени.

Идеально когерентных процессов нет и не может быть. Сами механизмы возникновения, распространения и регистрации излучения включают большое число факторов, нарушающих идеальность. Это протяженность, конечность любого реального излучателя, из-за чего экран по-разному «воспринимает» разные светящиеся точки. Любой элементарный осциллятор генерирует волну не бесконечно во времени: реальный световой поток - это набор цугов колебаний, «оборванных» во времени (имеющих начало и конец) да еще с непостоянной по длине цуга амплитудой. Иными словами, излучение всегда немонохроматично. Нарушения согласованности вызываются также доплеровскими эффектами, обусловленными температурным движением излучателей, неоднород-ностями и турбулептыостями в среде распространения.

Многие практические, задачи суперпозиции волн приближенно сводятся к задаче на стр. 32 (£ , £ =const, ол = Ш2, ei = e2 и Ai])=i])2-(i)i=const); это случай полной когерентности двух волн, в котором результат их интерференции однозначно определяется фазовыми соотношениями [см. формулу (1.49)]. Другой предельный случай - хаотическое некоррелированное изменение параметров двух волн (естественный свет) - определяется как полная некогерентность. Все реальные ситуации характеризуются большей или меньшей частичной когерентностью.

Основы современных математических представлений о когерентности света сформировались в 1930-1950-е гг., при этом введение количественных критериев опиралось на теорию интерференции

Количественной мерой когерентности двух световых колебаний (или двух точек волнового поля) служит функция взаимной когерентности £i2 или ее нормированное представление 712 - степень взаимной когерентности. Эти величины вводятся следующим образом. Интенсивность засветки произвольной точки экрана на рис. 1.8,6 определяется совместным действием волн Ei (-j-if) и и Е2(), где - разность фаз этих волн в произвольной точке М на оси X. Согласно (1.12) имеем

/,=<(Е,-ЬЕ,)(Е,-ЬЕ2)*) =

= (Е, Е;) + (Е2 Щ) -Ь 2 (Е, (-ьг),) EJ {t)). (1.59)

Для математических выкладок в (1.59) указание фазы в первых двух членах необязательно, так как для каждой из волн, рассматриваемых отдельно, начало отсчета времени может быть выбрано произвольным. Полагая в (1.59)

A.H)=<Ei( + f)E2(0>. (1-60)

учитывая, что <EiE*i>=/i и <Е2Е*2>=/2 есть интенсивности света в точке М, обусловленные источниками 5i и S2, и вводя нормированную функцию

окончательно получаем

1м = h + h + 2Re [Л, т = /1 + /2 + 2 , Re [у, {Щ. (1.62)

Подробнее рассмотрим функцию взаимной когерентности.

1. Из (1.59) и (1.60) следует, что £12(115) определяет ту дополнительную интенсивность А/12, которая обусловлена частичной когерентностью источников 5i и 52 и добавляется (разумеется, алгебраически) к сумме интенсивностей этих источников h+h] £i2(ij5) =A/i2/2. Введение нормировки дает удобный коэффициент

В этой связи часто встречающееся высказывание о том, что когерентные Еолны хорошо интерферируют между собой, представ.пяется по меньшей мере забавным, так как степень когерентности и определяется тем, насколько хорошо волны интерферируют друг с другом.

0 1 2 3 4 5 6 7 8 9 10 [11] 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119