
 | |
|
Слаботочка Книги 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 [112] 113 114 115 116 117 118 119 <? „ Вход Выход Рис. 10.13. Схема ВОЛС-ЗУ: Я - лазерный передатчик; ВС - волоконный световод; Я, - фотоприемник- Р - электронный регенератор; К - электронные коммутаторы; Яд - источники питания {---* - электронный поток; =ф- - оптический поток)
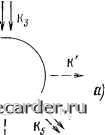 Считывание Л-5/0 -/-- Выход - Выход Рис. 10.14. Схема возбуждения фотонного эха в нелинейно-оптической резонансной среде (а) и временные диаграммы записи и считывания лог. 1 (б) и лог. о (в): луч Кб - спонтанное фотонное эхо ТО ее реакция (луч К4) будет отлична от реакции этой же системы без предварительного возбуждения. В этом и состоит суть явления: луч К4 представляет собой «эхо» предшествующих воздействий Ki « К2 (луч Кз стимулирует возникновение «эха»). В аспекте ЗУ Ki и Кг есть лучи записи (закодирован информацией может быть один из них, например Кг", тогда подсветка Ki представляет собой «питание»), Кз - считывания, К4 - луч единицы, Кз - луч нуля. Оценки показывают, что минимальный возбуждаемый объем кристалла может достигать 1 мкм, что соответствует плотности записи Ш" бит/см; скорость записи более 10 бит/с, время хранения - до нескольких минут. Чтобы реализовать эти возможности, должны быть созданы системы параллельного ввода-вывода информации, многоканальные лазеры пикосекундного диапазона, прецизионные оптические перестраивающиеся системы. Изложенный материал свидетельствует о больших достижениях оптической памяти (предсказываемых .ранее) и о практически безграничных ее потенциальных возможностях. 10.4. ОПТИЧЕСКИЕ ПРОЦЕССОРЫ В § 10.1 перечислены особенности оптоэлектроники, пригодные для использования в системах обработки информации. Реализация этих потенциальных возможностей идет по нескольким направлениям. Аналоговые оптические процессоры. Алгоритмическую основу этого направления составляет тот факт, что волновой фронт потока излучения, проходя через линейную оптическую систему, подвергается интегральному преобразованию в пространстве координат; в общем случае и)= f f Ф{х, у)Н{и, v; X, y)dxdy, (10.7) где Ф{,х, у) и F{u, v) - функции распределения поля в плоскости входной и выходной апертур; Н{и, v; х, у) - передаточная (переходная) функция системы (рис. 10.15). Если система линейна, то согласно принципу Гюйгенса - Френеля поле в любой точке на выходе формируется как результат суперпозиции (интегрирования) элементарных сферических волн, распространяющихся от каждой 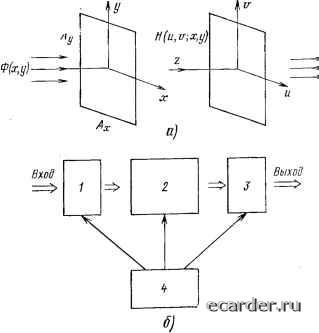 Рис. 10.15. Схемы преобразования световой волны в линейной и оптической системе (а) и оптического аналогового процессора (б): ху и ыт) - плоскости входной и выходной апертур вычислителя 2: 1, 3 - в.ходиое и выходное устройства; 4 - управляющее устройство точки поверхности входного окна системы. При осевой симметрии (система представляет собой сферическую линзу, набор круглых диафрагм, свободное пространство) в приближении параксиальной оптики для поля в дальней зоне (на бесконечности или в фокусе линзы, т. е. при z=f, где / - фокусное расстояние линзы) F (и, v)=lj Ф (X, у) ехр [2п i (, х + у)1 dx dy. (! 1.8) Здесь /а; и /j, - прострйнственные частоты выходного сигнала, которые при сделанных выше предположениях определяются как /, = и/л,* н fyv,/J (10.9) Пространственные частоты имеют размерность мкм~; в общем случае любой оптической системы выражения для них более сложные, чем (10.9). Физически (10.9) характеризует периодичность распределения максимумов поля излучения при дифракции на круглом отверстии (см. гл. 1). Выражение (10.8) представляет собой двухмерное интегральное преобразование Фурье функции Ф{х, у) в пространстве координат (т. е. фурье-образ функции Ф{х, у)), подобное преобразованию сигналов во вре.менной плоскости, часто встречающемуся в радиотехнических задачах. Функция Я, называемая также импульсным откликом системы, физически представляет собой выходное изображение, формируемое точечным входным источником, т. е. сигналом вида Ф{х, y)=6(xt, уг), где 6 - дельта-функция, не равная нулю при x=xi и y=yi- Выражение (10.8) справедливо для линейных систем лишь в том случае, если они обладают свойством инвариантности (изолланар-ности) по отношению к смещению, т. е. если форма выходного изображения не зависит от пространственных перемещений в.ходного изображения. Строго это выполняется для параксиальной оптики; в других случаях, как правило, удается входную апертуру разделить на участки, в пределах которых система практически изопла-нарна. Итак, при сделанных предположениях общий результат, даваемый уравнением (10.8), состоит в том, что изображение на выходе системы есть двухмерный фурье-образ функции ее пропускания. Если излучение когерентно, то входящие в (10.8) величины описываются комплексными функциями вида Ф (лг, у) -. Ф« {X, у) ехр [i ф (х, у)\, (10.10) где действительная часть Ф°{х, у) несет информацию, заложенную в амплитуде световой волны, а действительная функция cp(.x;, у) описывает информацию, заложенную в фазе волны. Функция Ф{х, у) представляет собой, таким образом, комплексную амплитуду когерентного светового поля. Преобразование (10.8) осуществляется в комплексной плоскости; физически оно определяет и изменение амплитуды, и сдвиг фазы, зависящие от взаимного пространственного расположения рассматриваемых точек входа и выхода. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 [112] 113 114 115 116 117 118 119 |
||||||||||||||||