|
| |
|
Слаботочка Книги е, (1.16) котором со меняется непрерывно в некотором интервале (в общем случае 0<со<оо). 3. Скорость распространения волны (1.8) равна с/]/ер, или с учетом фундаментального соотношения Ущх=--п, (1.14> где п - показатель преломления среды, с/п (в вакууме при в= = [1=п=1, естественно, с). Она представляет собой фазовую скорость волны \ф, т. е. скорость перемещения в пространстве одинаковых по фазе точек волны (например, точек, соответствующих максимуму напряженности Еу = Еуо). Характеристические параметры монохроматической световой волны связаны простыми соотношениями к= -е= - е; oj = 2nv= - , (1-15) с пк где V, % - частота и длина волны световых колебаний соотвгт-ственно. Если распространяющаяся волна представляет собой совокупность монохроматических волн с различными значениями oj и к, то для ее характеристики используется понятие групповой скорости волны Vr, совпадающей со скоростью переноса энергии. Если со и к для группы волн не сильно отличаются друг от друга, то где ko - волновое число, соответствующее «центру» группы. Для монохроматической волны Уг=Уф, в произвольном случае соотношения между Пф и Vr могут быть различными, но всегда vc/n, т. е. скорость переноса энергии не может превышать скорость света в среде. 4. Поперечные (и только поперечные) волны обладают изначальным по самой природе присущим им свойством поляризации, т. е. неэквивалентностью различных направлений в плоскости, перпендикулярной лучу. Представленная на рис. 1.3 волна, у которой колебания электрического вектора фиксированы в одном направлении, является линейно поляризованной: направление вектора поляризации совпадает с вектором Е, а плоскость поляризации перпендикулярна ему. В более общем случае (например, суперпозиция двух волн Е] = Еу{х, t) и Еч, = Ег{х, t), распространяющихся в направлении х и имеющих взаимно ортогональные электрические векторы) монохроматическая волна является эллиптически поляризованной: за каждый период колебаний конец вектора Е описывает эллипс в проекции на плоскость yz на рис. 1.3. В частном случае при Eyo = Ezo имеет место круговая поляризация. Если при распространении волны направление колебаний вектора Е хаотически беспрерывно изменяется и любые его положения в плоскости yz оказываются равновероятными, то такая волна является неполярпзованной (используют термин естественный свет). Если световой поток частично поляризован (что чаще всего и встречается), т. е. его электрический вектор имеет некоторую преимущественную ориентацию (или преимущественный закон изменения); то для количественной характеристики такого потока вводится степень поляризации Л = /,/(/„-Ь/,), (1.17) где /п, /е - интенсивности поляризован;юго и естественного компонентов света. Очевидно, что Л изменяется от О до 100%. Элементарные (атомные) классические излучатели - электрический дипольный осциллятор (колебахшя электрона в поле ядра) или электрический ротатор (вращение электрона вокруг ядра) - генерируют линейно и эллиптически поляризованные волны соответственно. Однако в совокупности эти излучатели эффекта поляризации не дают. Понятно, что-для его восстановления нс--обходимо обеспечить анизотропию среды, при которой была бы установлена ориентация элементарных излучателей, как это, например, имеет место практически во всех кристаллах. Поляризация излучения лазера обеспечивается анизотропией оптического усиления, обусловленного избирательностью резонатора Фабри - Перо. В заключение еще раз подчеркнем, что проведенное в этом параграфе рассмотрение характеризует электромагнитные волны, распространяющиеся в безграничной, изотропной непоглощающей среде. 1.2. РАСПРОСТРАНЕНИЕ ВОЛНЫ ИЗЛУЧЕНИЯ В РЕАЛЬНОЙ СРЕДЕ Выясним, к каким изменениям решения уравнений Максвелла приведет учет неидеальностей, имеющих место в реальных условиях распространения световых волн. Прежде всего очень часто приходится учитывать то, что оптическая среда небезгранична. Типичные примеры этого - распространение излучения по волоконно-оптическим световодам, имеющим цилиндрическую симмет-:рию, или по плоским интегрально-оптическим диэлектрическим волноводам. В обоих случаях поперечные размеры оптических сред соизмеримы с длиной волны света Я, протяженность же среды вдоль направления распространения можно считать бесконечной. Другой пример - распространение световой волны внутри .лазера. Здесь необходимо учитывать наличие границ по всем трем координатам, т. е. мы встречаемся с задачей возбуждения объемного резонатора. Рассмотрим однородный бесконечно протяженный волновод (рис. 1.4), у которого обозначим через 2 контур, ограничивающий это сечение. Решать уравнения Максвелла удобно, пользуясь по-.дяризационным потенциалом (или вектором Герца) Пг, связанным с вектором-потенциалом А [см. формулу (1.6)] простым со-отношением A=-L. (1.18) с dt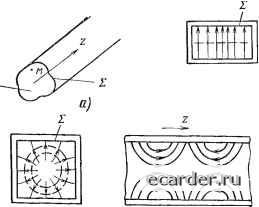 
 Рис. 1.4. К распределению излучения в оптическом волноводе: а - обобщенная модель волновода; б, в - структуры полей в волноводах с прямоугс-ьным поперечным сечением (непрерывные линии - силовые линии электрического поля /АХ;,;, штриховые - силовые линии магнитного поля ТЕю) Если положить, что поля в волноводе меняются по периодическому закону ехр(-/со/), омических потерь нет (а=0) и вектор П,-имеет лишь один компонент, направленный вдоль оси z, то решение может быть представлено в виде /7р (М, г, О = 1 (М) / (г) ехр {-1 со i), (L19> где М - произвольная точка, лежащая в поперечном сечении s, имеющая координаты и у; ф(М) -собственная функция задачи о колебаниях мембраны, закрепленной по контуру, т. е. г)52 = 0, (1.20) имеющей бесконечную систему собственных значений {ат} и собственных функций {tlim}. Частные решения г-составляющей вектора Герца fm{z) определяются из уравнения (1.21) Для волны, распространяющейся в положительном направлении оси Z, L = A„,exp(iVk-amz) . (1.22). Общее решение уравнения Максвелла для волновода на рис. \А,а, представляющее собой суперпозицию всех частных решений, имеет вид: /7г(М.г,0= f A4\n{M)expl~i{cot-Vz)]. (1.23). 0 1 2 3 4 5 [6] 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 |
||||||||||||