Слаботочка Книги

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 [93] 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119

.дечнику длина волны излучения уменьшается в ni раз. С учетом сказанного получаем, что в типичном двухслойном световоде с dc = 50 мкм и МА=0,2 при л = 0,8 мкм число направляемых мод УИл;2000. Для реализации в световоде одномодового режима для лазерного излучения с л=1,3 мкм требуется при NAO,l диаметр сердечника dc<7 мкм.

Анализ частных решений волнового уравнения (волноводных мод) показывает, что они описываются функциями, монотонно спадающими (обычно экспоненциально) к периферии сердечника, но в то же время не обрывающимися на границе сердечник - оболочка (рис. 9.2). Иными словами, направляемые моды частично просачиваются в оболочку, т. е. отражение происходит не на геометрической поверхности раздела, а в некоторой приповерхностной области (рис. 9.2,а). Расчет показывает, что для направляемых мод с малыми углами падения (распространяющихся при малых значениях V) доля мощности, переносимая по оболочке, может быть значительной: для То-моды при V=l она составляет 70%, а при У = 2,4 - всего 16%). Характерно и то, что при У= 1 поле 7£о-мо.а.ы проникает в оболочку на глубину порядка dc. Отсюда, в частности, следует важность чистоты не только сердечника, но и оболочки для маломодовых (и особенно одномодовых) волокон, а также необходимость достаточно большого диаметра оболочки (с?о>Зс?с).

Расчет дисперсии. Основное практическое приложение модовой теории - это расчет дисперсионных характеристик волокон различного типа. Наиболее наглядные выражения удается получить при анализе расплывания б-импульса. Так, интегрированием решения волнового уравнения для многомодового двухслойного ступенчатого световода получено

Оов = Ап/(2 1/Зс). (9.9)

Используя переводное соотношение (9.1), получаем то~0,14А/р„-о, что согласуется с качественными представлениями лучевой теории.

Дисперсия градиентного световода зависит от конкретного вида функции n=f{r). Обычно при расчетах задаются следую-

	,
/ / 1

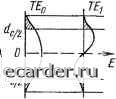Рис. 9.2. «Просачивание» каналируемого излучения в оболочку:

а - модель лучевой теории; б - модовая структура поля для ГЕо- и 7"£-мод

щей формулой, удовлетворительно описывающей практически: все возможные типы существующих градиентных световодов:

„ (,) = f Hi [ 1 - 2 Д (2 ;-/4П>/2 при г < d,/2 ;

1 «2 при г > 4/2,

где Д=(/г=1-яг)/2=1 (ni-«г)/я1 - относительная разность показателей преломления; а - постоянный для данного вида световода показатель, которым можно управлять технологически;. «I, «2 - показатели преломления центра сердцевины и оболочки.

Для наиболее распространенного случая параболического изменения показателя преломления (при а л; 2, когда (9.10) принимает вид п{г) ;п,.[1-A(2r/dc)=])

a„,= l = -iMi .„ = 2, (9.11>

где An-til-П2. Детальные оценки показывают, что случай а = 2 не является оптимальным; наибольшее приближение к самофокусировке достигается при

а„п, = 2-12д/5. (9.12).

При этом

(ToB = «iA/(20 КЗ с), « = (9.13>

Характерно, что лля градиентных световодов дисперсионные константы пропорциональны (Дп), тогда как для волокон со ступенчатым профилем показателя преломления они пропорциональны An. При условии Дп<С 1 становится очевидным преимуществен градиентных волокон. Численные оценки по (9.9)-(9.13) показывают, что при Лп=0,02 приведенное уширение импульса составляет 20 нс/км для двухслойного световода, 130 и 15 пс/км для градиентного параболическо! о (а 2) и оптимизированного-(аопт~1,97). Отсюда следует, в частности, что оптимизация достигается лишь при очень высокой -ючности реализации требуемого значения «опт-Минимальные приведенные значения экспериментально получить не удается из-за дисперсии материала. Приведенная к единице длины постоянная времени материальной дисперсии приблизительно одинакова для всех волноводных мод и зависит лишь-от ширины спектра излучения и дисперсионных свойств материала:

Используя (9.1), можно при необходимости перейти от том к оом. Экспериментальная дисперсионная кривая для кварца, легированного фосфором (материал сердечника практически всех основных типов световодов для ВОЛС), представленная на рис. 9.3,. показывает, что при Kl,S мкм дп/дКО и соответственно тон==

283-.

= 0. Именно этим прежде всего и определяется значимость спектральной области вблизи Л,= 1,3 мкм.

Расчет показывает, что в многомодовых световодах эффекты шнутримодовой дисперсии оказываются пренебрежимо малыми по сравнению с другими видами искажений и, в час-нос~и, с дисперсией материала. Поэтому, переходя к общей оценке, внутри-модовую дисперсию не учитываем.

Рассмотренные эффекты - волноводная и материальная дисперсия - действуют одновременно; решение задачи уширения импульса при этом резко усложняется: наряду с членами, которые приводят к значениям оов и оом, появляется еще суперпозиционный член /(оов, оом). В первом приближении можно считать, что суммарное уширение импульса

ов> "oм• (9.15)

Характерно, что оов и оом не соответствуют в точности значениям, получаемым из (9.11), (9.13), (9.14). Приведенные на рис. 9.4 расчетные кривые иллюстрируют сказанное и позволяют сделать следующие выводы: при учете двух механизмов дисперсии значение аопт заметно сдвигается относительно точки ал2; в градиентном световоде, возбуждаемом светодиодом, уширение импульса почти полностью определяется материальной дисперсией и оптимизация профиля п по а заметных преимуществ не дает; в оптимизированном многомодовом градиентном световоде, возбуждаемом монохроматическим лазером, дисперсионное уширение импульса может быть снижено до 15 пс/км (теоретический пре-.Дел).

бц, пс/нп

-fA/c)(dn/dx),nc/{m-m) 200 \-\ 150 Ш

О -50

-1-L.

0,Е 1,0 А, мнм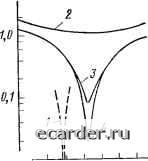

0,01 и.

1,Б 1,8 2,0 2,2 2,it 2,6 2,8а

Рис. 9.3. Спектральная характеристика дисперсии кварца

Рис. 9.4. Теоретическая зависимость

00 от параметра а градиентного све-

товода:

1 - учитывается только модовая дисперсия; 2 -A?v=I5 нм (светодиод); 3 -ДЯ.= = 1 нм (инжекционный лазер); 4 -ДЯ.= =0,2 нм (лазер с распределенной обратной связью); кривые 2-4 рассчитаны для

Я=0,9 мкм

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 [93] 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119