Слаботочка Книги

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 [95] 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119

венно ускоряется при наличии механических деформаций и химическом действии тех или иных реагентов, главным образом влаги и кислорода, устранить влияние которых практически невозможно.

Подводя итоги, можно расписать общее выражение (9.18) следующим образом:

+ ион + ОН + техн + Ькаб "Ь 6 + + Д- (9-20)

Отметим, что пользоваться (9.20) практически невозможно: большинство его составляющих не рассчитываются и характеризуются индивидуальной спектральной зависимостью. Типичный спектр поглощения высокочистого кварцевого световода (вне кабеля) представлен на рис. 9.5, где наглядно отражены закономерности релеевского рассеяния и пики, связанные с ОН группами; видно также наличие трех окон прозрачности вблизи длин волн 0,85; 1,3 и 1,55 мкм и преимущество длинноволновых окон.

Пределы применимости. Представленные в этой главе физическая картина и расчетные соотношения справедливы как некоторое приближение к действительности. Имеются ограничения, которые вытекают непосредственно из рассмотренной теории илн как следствие из неучтенных физических эффектов.

Ранее указывалось, что при У= 1 до 70% мощности направляемой моды вытекает в оболочку, т. е. исходные качественные представления о распространении излучения по световоду теряют смысл. Условие dc=(2...5)K определяет геометрический предел представленной теории.

Детальный анализ процесса отражения распространяющегося излучения на границе сердцевина - оболочка приводит к заключению, что имеется большое число мод, которые нельзя однозначно отнести ни к направляемым, ии к вытекающим модам. Для таких слабовытекающих мод (геометрически - очень косые лучи) проникновение поля в оболочку не является малым и волну нельзя рассматривать как полностью направляемую, в то же время потери не настолько велики, чтобы считать ее ненаправляе-мой. Теория этих мод еще недостаточно разработана.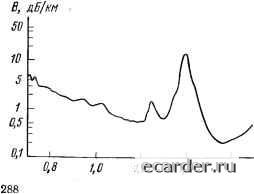

1,ВХ.мкн

Рис. 9.5. Тип75чный спектр поглощения кварцевого световода

Существование слабовытекающих мод определяет два других ограничения теории. Во-первых, требование к конечности толщины оболочки, которое формулируется как (1,5 ... 2)с?с для многомодовых и rfo (3... 10)(ic для одномодовых световодов. При меньших значениях do представленные выше расчетные соотношения начинают существенно нарушаться. Во-вторых, учет слабо-вытекающих мод дает в (9.20) дополнительный компонент потерь, который при малости всех остальных составляющих может стать определяющим. Иными словами, устанавливаются пределы применимости формулы (9.20).

Искажение представленной картины и нарушение большинства расчетных соотношений возникает и при очень значительных плотностях мощности каналируемого излучения; причина этого - нелинейные оптические явления (см. гл. 3). Эффекты вынужденного рассеяния Мандельштама - Бриллюэна и Рамана приводят к «повороту» значительной части потока назад - феноменологически это проявляется в резком возрастании затухания. Нелинейно-дисперсионные явления проявляются в обострении фронта светового импульса [в противоположность (9.15)] и в возбуждении солитонного режима. Пороговое значение плотности мощности для кварцевых световодов 10... 10 Вт-см"2, но заметное проявление нелинейных эффектов может наступить и значительно раньше.

При анализе градиентного световода использовался параметр а, однако фактически профиль показателя преломления описывается волнистой кривой, имеющей локальные всплески и спады (в частности, типичен провал п в центре световода). Оценки показывают, что отклонение от идеализированной кривой всего на 2... 3% может привести к изменению дисперсионной константы для оптимизированного градиентного световода чуть ли не на порядок. Этими цифрами и устанавливается предел целесообразного уточнения значения Оопт.

Наконец, следует отметить статистический подход, лежащий в основе многих проведенных расчетов: релеевского рассеяния, межмодовой связи и др. При этом естественно возникновение шумов, ограничивающих минимальный уровень мощности оптических сигналов, надежно передаваемых по световоду.

9.2. ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ ВОЛС

Элементную базу ВОЛС составляют волоконно-оптические кабели, передающие и приемные оконечные устройства (модули), оптические соединители, разветвители, коммутаторы. Именно из этих аппаратурных средств создаются системы оптической связи. Но каждый из названных элементов представляет собой сложное

* Это обратное рассеяние, в особенности рассеяние Мандельштама - Бриллюэна, позитивно используется как прецизионный «инструмент» исследования характеристик световода вдоль его длины.

устройство, в свою очередь состоящее из нескольких комплектующих элементов, свойства и характеристики которых в конечном счете определяют возможности ВОЛС. Эти оптические, опто-, микроэлектронные, оптико-механические элементы (изделия, материалы) также входят в элементную базу ВОЛС.

Оптические волокна. Определяющими в технике ВОЛС являются кварцевые двухслойные волокна трех основных разновидностей: многомодовые ступенчатые и градиентные, а также одномо-довые (рис. 9.6,а-в). В одномодовых волокнах закон изменения показателя преломления внутри сердцевины неважен, поэтому эти волокна, как правило, близки к ступенчатым. Показанный на

50...WDMIIM .dg=2,5d.

dn5D...6DMHH

Tti-nf~0,D2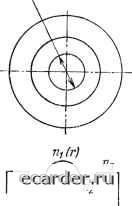

df, = 3...7mn

й(,гт...тмт

Полипвр

dc-lD... 250тм d=m... 1000 mm do-(1,1...1,5)d,

NA=D,2-D,55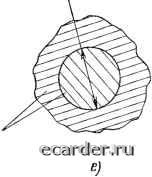

Полимеры

Рис. 9.6. Геометрия и профиль изменения показателя преломления кварцевых двухслойных многомодовых ступенчатых {а), градиентных (б), одномодовых (в) волокон. Геометрия сердцевины и числовые апертуры кварц-полимерных (г), из многокомпонентных стекол {д) и полимерных (е) световодов

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 [95] 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119