
 | |
|
Слаботочка Книги 0 1 2 3 4 5 6 7 8 9 10 11 [12] 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 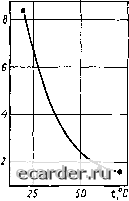 -П,% Wfi
200 t,°C Рис. 28. Зависимость Рис. 29. Зависимость от температуры часовой времени релаксации щ ползучести тензорезнсторов 1-ВО после тепловой от температуры для тен- обработки при различных температурах, °С: ЗОреЗИСТОрОВ 1-П с ба---160; -----ISO; -------200; ЗОЙ 10 мм ---Д----250 (-1-ь1)Х10~ °С~] приводят к уменьшению по абсолютной величине daxl[a\dt) и daUadt) не более чем на 1%/°С. Большие снижения времен релаксации происходят за счет вязкостей т]2 и цзу входящих во вторые члены уравнений (85). Причем на изменение ai и аг от температуры влияют постоянные полимера w, Wi (энергии активации). Для полимеров с сильными межмолекулярными связями значения w и Wi существенно больше, чем для полимеров, молекулы которых связаны слабо. Температурный коэффициент времен релаксации oi и 02 за счет влияния w н Wi обратно пропорционален квадрату абсолютной температуры и зависимости ai=f{t) и а2=/(/) нелинейно уменьшаются с температурой, что подтверждается экспериментальными данными (см. рис. 27 и 28). Однако количественно оценить расчетным путем зависимость от температуры времени релаксации за счет влияния второго члена уравнений (85) затруднительно вследствие отсутствия данных о значении констант w и Wi для полимерных материалов, используемых в качестве связующего. Можно отметить, что для полимерных материалов в работах [3, 60 и др.] для щ и 02 также приводится экспоненциальная зависимость от температуры, что подтверждает сказанное выше об основном вкладе изменения вязкости в температурные коэффициенты времен релаксации oi и ог в уравнениях ползучести тензорезнсторов. Зависимость ползучести от температуры, определяемая влиянием температуры на упругие и вязкие константы связую- щего, может быть уменьшена предварительной тепловой обработкой тензорезнстора, приводящей к изменению значений Gi, Ge, т]2. Лз (см. п. 2 гл. 3).Так, на рис. 29 приведена зависимость ползучести тензорезнсторов 1-ВО, подвергаемых после наклейки тепловой обработке по различным режимам. Наименьшую зависимость ползучести от температуры имеют тензорезисторы 1-ВО, прошедшие тепловую обработку при 250°С, т. е. на 50°С превышающую максимальную температуру испытания. Такие же рекомендации по уменьшению влияния на ползучесть путем тепловой обработки при температуре, на 30-50°С превышающей рабочую, приводятся и для других типов тензорезнсторов [25, 76]. 3. МЕХАНИЧЕСКИЙ ГИСТЕРЕЗИС ТЕНЗОРЕЗНСТОРОВ Механический гистерезис тензорезнсторов определяется как разность выходных сигналов н при возрастании и р при уменьшении деформации, полученная при одних и тех же значениях деформации детали, на которой установлен тензорезистор, т. е. Г=р-н или в относительных единицах Г-=($р-$Ж, (86) где 1т - выходной сигнал при максимальном ет значении деформации. Из теории полимеров [3, 60] известно, что гистерезисные явления в них определяются различными причинами, важнейшими из которых являются релаксационные процессы, связанные с временными процессами вязкоупругости и текучести. Такой вид гистерезиса проявляется при любом цикле нагружения-раз-гружения. Кроме этих явлений гистерезис в полимерных связующих может определяться также механическими процессами, связанными с разрушением молекул и молекулярных связей, а также тепловыми эффектами при деформации. Однако механохимические процессы проявляются только в первом цикле нагружения-разгружения и при последующих циклах гистерезис этого вида существенного значения не имеет, а вклад тепловых эффектов при деформациях практически невелик. Рассмотрим расчет механического гистерезиса тензорезнсторов, связанный с временными релаксационными процессами вязкоупругости и текучести, приводящими, как и при рассмотрении ползучести, к уменьшению возникающих при передаче деформации сдвиговых напряжений. Принимая, что выходные сигналы тензорезнстора пропорциональны этим напряжениям, можно уравнение (86) написать в виде Г== (5р-5н)/5:„, где 5н, 5р и 5;„ - напряжения, возникающие в связующем при увеличении и уменьшении деформаций и при ее максимальном значении е. 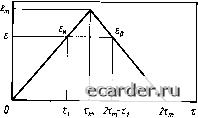 Рис. 30. Деформация балки при иа-груженин и разгружении ее с одинаковой скоростью R Гистерезис вызывается теми же релаксационными процессами и для определения этих напряжений следует воспользоваться теми же механическими моделями и реологическими уравнениями, которые используются при расчете ползучести. Для определения гистерезиса нагружение и разгружение балки с тензорезисторами проводят с одинаковой скоростью. Соответственно при этом деформация е поверхности балки будет изменяться в том же темпе и может быть представлена графиком (рис. 30) или уравнениями, выраженными через время т: на ветви возрастания деформации на ветви уменьшения деформации (87) (88) (89) где R - скорость изменения деформации. Рассмотрим случаи, когда связующее не обладает текучестью (т1з=оо), что соответствует механической модели (см. рис. 19, б) с реологическим уравнением (68). Считая, что е=у и подставляя в него ен и ер, получаем при возрастании деформации dS„ , 0 + 0s, = -Rx+G,R, (90) 12 12 а при уменьшении деформации dx 1)2 12 г,-/?г)-ед (91) Решение же дифференциальных уравнений (90) и (91) с учетом формул (65) и (76) будет (92) 5,=G,/?t-f((7,-G,)/?a,U-e j; 5р = G, (2s„ - Rx) -f (G, - Ge) Ra, (2e i - e ") . При измерении гистерезиса, когда ен=ер=е (см. рис. 30), уравнении (92) время t=ti, а в уравнении (93) т=2тт-ть Отсюда при ен=ер=е, учитывая формулы (88) и (89) и то, что Гт=ет1Я, получзем: 5„=G,£--(G,-Ge)/?a,il-e ; (94) 5p = G,£-f(Gi-Ge)/?a,L2e -1-е (95) Выразим уравнения (94) и (95) через мгновенное Smo сразу после нагружения до Вт и установившееся Sme напряжения, которые для механической модели, приведенной на рис. 19, б, будут 5o = Gie, 5, = G,s„. Преобразуя формулы (94) и (95), получаем: 5р = Ra, 1-е а гистерезис Гк, обозначенный для этого случая по аналогии с Пк, с учетом формулы (86) составляет Гк = - Rai 2-е "-2е -f е 2s -« .2е -f е Так как гистерезис и ползучесть определяются одними и теми же релаксационными процессами в связующем, то целе сообразно выразить гистерезис через установившееся значение ползучести Пе, которое можно представить в виде Пе = (5,0-5,„е)/5„0- Тогда = -URaJ2-e~- Напряжение 5то в связующем, возникающее при быстром (практически мгновенном) нагружении до Вт, всегда больше напряжения 5, возникающего при нагружении с меньшей скоростью. Однако для связующих, используемых в тензорезисторах, можно считать, что отношение Smo/Sm близко к единице, и тогда / • «™-« 2s„-«\ Г ПеЛа! -- " -2e -fe (96) 77 Как следует из уравнения (96), гистерезис определяется установившимся значением ползучести Пе, а также временем релаксации связующего оь скоростью изменения деформации R, максимальным ет и текущим е значениями деформаций. Зависимость Пе от различных параметров тензорезнстора определена в п. 2 гл. 3. Для удобства рассмотрения влияния ai, /?, Em и е на гистерезис тензорезнсторов обозначим сомножитель, зависящий от этих факторов, через безразмерный параметр хь который можно представить в виде Rai (97) и тогда Гк=-ПеХ1. (93) Из анализа уравнения (97) следует, что при заданном еЫт значение xi определяет безразмерный параметр Eml(Rai), обозначенный нами через vi, т. е. vi=ej(/?a,), который является отношением времени нагружения Тт ко времени релаксации oi. Уравнение (97) удобнее представить в виде I L (99) Если VI постоянно, то параметр хь а соответственно и гистерезис Гк при заданном значении в/ет также должны быть постоянными. Экспериментальные значения гистерезиса Го (при е=0) тензорезнсторов ФК, 1-Пн и КМ, полученные в условиях нагружения до различных вт за одинаковое время Хт, подтверждают это предположение. Так, на рис. 31 приведены в за- 0,02 О -0,02 -0,10 -0,12
о 250 500 750 1000 1250 1500 1750 £„,м/1Н- Рис. 31. Гистерезис Го (при е=0) тензорезнсторов, нагружаемых до различных Вт за одинаковое время т висцмости от деформации вт средние значения Го для партий из 12-20 фольговых тензорезнсторов ФК, проволочных 1-Пн и полупроводниковых КМ. Для каждого типа тензорезнстора можно считать ai = const, а соответственно в этих экспериментах при всех нагружениях vi = const. Как следует из рис. 31, средний в партии гистерезис для каждого типа тензорезнстора при вариациях вт от 0,1 до 2-10 практически одинаков. Гистерезис Гд, связанный с текучестью, как и ползучесть Пд, определяется из рассмотрения механической модели, приведенной на рис. 19, в, и решения реологического уравнения (71) при значениях ен и ер, определяемых формулами (88) и (89) соответственно. Решение уравнения дает: Проведя аналогично выводу Гк подстановки и преобразования, а также учитывая выражение (65) и принимая с допущениями, рассмотренными ранее, что 2m> получим 2 е "« - 26 п4-е . (100) Суммарное же значение гистерезиса будет Г=:Гк-ЬГ.=-(ПеХг+Х2). Для удобства использования расчетных формул (99) и (100) можно представить их в виде серии графиков (номограмм), рассчитанных при значениях 1-в/вт, которые откладываются по оси абсцисс (рис. 32). Как следует из графиков, по мере возрастания v до 1,0- 2,0 значения % при заданных значениях 1-в/вт увеличиваются примерно до 0,5, а затем начинают уменьшаться. Такая зависимость %-fi\) связана с тем, что при очень больших скоростях нагружения, когда Bm/R<a, релаксационные процессы в связующем от высокоэластичности и текучести не успевают 0 1 2 3 4 5 6 7 8 9 10 11 [12] 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||