
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 [117] 118 119 120 121 122 123 124 125 126 127 128 129 130 а для абсолютных значении переменных Хг. i = х2 i-i + i. (10-25) Для исследования дниамикн нелинейной системы управления с помощью ЦВМ иа базе рассмотренного алгоритма без итераций составляется программа в соответствии со структурной схемой, приведенной на рис. 10-28. Составление программы Производится в следующей последовательности. Прежде всего определяе1ся математическая модель системы в форме уравнений состояния (дифференциальных н алгебраических). Затем проводится анализ математической модели с целью выяснения формы записи функциональных входных воздействий и статических характеристик звеньев (аналитическая, графическая или табличная) и вида математической модели (характер уравнений: дифференциальные, алгебраические или нх комбинации). Составляется программа иа проблемно-ориентированном языке с учетом проведенного анализа н в соответствии с выбранными методами численного интегрирования и интерполяции (см. ниже). На рис. 10-28 структурная схема представлена для нелинейной системы, математическая модель которой состоит из п дифференциальных уравнений, с целью решения задачи иа базе алгоритма последовательного типа без итераций, В общем виде вычислительная процедура для рассматриваемого случая состоит в следующем. 1. Вводятся исходные данные (оператор j) и начальные условия для всех переменных: х; л:. ; Хп.а, начальное время счета Т = О, конечное время счета Гц, значения входных воздействий при t = 0. 2. Производится вывод таблицы текущего времени, входных воздействий и значений переменных состояния (оператор 2). 3. Вычисляется текущее время (оператор 5). Ф*.. (О 4. Вычисляются значения входных воздействий Ф*, м (О + д по аналитической формуле, еслп функция ф (/) задана аналитически (оператор 4). Если функция ф (i) за-йиa в виде таблицы или графика, то необходамо предусмотреть ращение к подпрограмме интерполяции (оператор 5), в которой лчисляется необходимое значение каждого входного воздей-9рия на рассматриваемом шаге интегрирования (оператор 6). пом *ледует иметь в виду, что в подпрограмму интерполяции оми.мо програм.мы аппроксимации нелинейных функций входит *к*е массив узлов интерполяции. 5. Вычисляется значенне приращения переменной Дх, по фор, муле (10-24) (оператор 9), если все переменные, входящие в правую часть дифференциальных уравнений, заданы аналитически. В противном случае происходит обращение к подпрограмме интер! поляции (оператор 7) и вьечисляются значения тех переменных которые были заданы таблично (оператор 8), после чего вычисляется приращение Axi. Ввод данных Выдод та5лии.ы г<г> Г<!> Вычисление Обращение к подпрограмме интерполяции гт®- Повпрограмна интерполяции Вычисление AXi по (10-24) Xi=X(+Axf Обращение к подпрограмме интерполяции Йадпрогранма интерполяции Рис. 10-28 Обращение к подпрограмме интерполяции 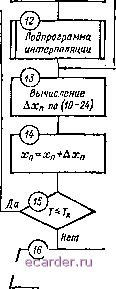 ВыВод }та5лицы конечны даннык Конец 6. Вычисляется значенне переменной Xi в конце шага интегрирования по (10-25) (оператор J0). 7. Аналогично вычисляются приращения и абсолютные значения переменных состояния Xg, .... х (для х операторы 11-14). 8. Проверяется условие Т Тк; если оно выполняется, происходит переход к оператору 2 для вычислений иа следующем щаге интегрирования. Если вычисления на заданном отрезке времени выполнены полностью (Т > Т), то осуществляется переход к операторам J6 и Конец . 10-7-2. АЛГОРИТМ С ИТЕРАЦИЯМИ (ВТОРОЕ ПРИБЛИЖЕНИЕ) В соответствии с формулой (10-22) вычислительный алгоритм для определения приращений переменных состояния с итерациями в системе уравнений (10-23) будет иметь вид xf,=мфг.i-d)+Щ..... Ф,. (0+ < A4i = Ath Ф1,(t) + ..., ф ,(О -f Xi. i-1 -J--2- <Рх, .-1 (О +%,.... Ф.,ы (О i--2-.....--2~ A-i!>< = т \<ег.(О+.....Ф , it)+smM. . X i-i -\- (10-26) форму* значения переменных состояния вычислякяся по Hemfp/ приведена структурная схема программы для в по исте.мы, чатематнческая модель которой так же, как Редыдущем случае, состоит нз п дифференциальных уравнений 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 [117] 118 119 120 121 122 123 124 125 126 127 128 129 130 |