
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 [118] 119 120 121 122 123 124 125 126 127 128 129 130 ввод данных r=0;T;(o(t)i 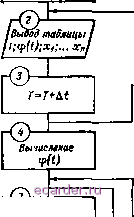 Обращение к подпрограмме интерполяции Подпрогрсшт антераомяцаа Вычишнив Дх по (10-24) Обращение к подпрограмме интерполяции Т<2> Подпрограмма интерполиции г(£) Одращвниа к подпрограмма интерполяции Подпрограмма интерполяции Рос. 10-29 Вычисление Дхл во (10-24) Оращенае к подпрограмме интерполяции fT<S> программа интерполяции Вьтсденав Дас, по (10-2Б) г®- Вычисление Обращение к подпрограмме антерполяцаа 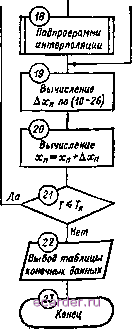 для решения задачи на базе алгоритма последовательного типа ситерациями. Программа составляется в последовательности, описанной в пре-идущем случае. Она несколько отличается от программы вычислений без итераций. В общем виде вычислительная процедура для рассматриваемого случая состоит в следующем 1. С по 9-к оператор вычислительная процедура идентична предыдущему случаю (рис. 10-28), т. е. осуществляется ввод исходных данных и начальных условий, производится вывод таблицы данных, вычисляется текущее время, входное воздействие п лри-ращенне переменной х 2. Поскольку при расчете по итеративной формуле в вычислении абсолютного значения переменной на промежуточных стадиях расчета нет необходимости, то в структурной схеме программы рис. 10-29 осуществляется непосредственный переход к вычислению значений приращений остальных переменных (для Ах операторы 10, 11, 12). При этом следует иметь в виду сказанное выше о возможности двух путей решения: с обращением и без обращения к подпрограмме интерполяции 3. Вычисляется приращение переменной Длт по формуле (10-26), что представляет собой второе приближение (оператор 15), если все- переменные, входящие в правую часть дифференциального уравнения, заданы аналитически. В противном случае предварительно происходит обращение к подпрограмме интерполяции (операторы 13, 14). 4. Вычисляется значение переменной в конце шага интегрирования (оператор Щ по формуле (10-27), так как обычно прн практических расчетах производить более двух итераций нецелесообразно. 5 Аналогично вычисляются приращения и их абсолютные значения для остальных переменных (для Хп операторы 17-20). 6. Проверяется условие Т Т, и, если оно выполняется, происходит переход к оператору 2 для вычислений на следующем шаге интегрирования. Если выч1!слеиия на заданном отрезке врейеш! выполнены полностью (7 > Т ), то осуществляется переход к операторам 22 н Конец . При вычислении с итерациями на базе алгоритма последовательного типа отпадает необходимость в прометку точном вычислении абсолютных значений переменных (структурная схема рис. 10-29), что имеет место при пользовании итеративными методами параллельного типа (например, методом Эйлера-Коши). ото обстоятельство является особенностью алгоритма последовательного типа. Основное достоинство программ, составленных по структурным схемам рис. 10-28 и 10-29. заключается в том, что в них отсутствует избыточность (полное соответствие вычислительным алгоритмам), что ведет, к сокращению затрат машинного времени, днако это достоинство влечет за собой и определенный недостаток, заключающийся в том, что для каждой конкретной задачи программа ее решения составляется заново. Даже изменение коэффициентов уравнений, описывающих систему, ведет к изменению программы. 10-7-3. СТАНДАРТНАЯ И РАБОЧАЯ ЧАСТИ АЛГОРИТМА С целью устранения указанного выше недостатка применяется структурная схема алгоритма, состоящая из двух частей; стандартной и рабочей. Первая часть (стандартная) интерпретирует вы- 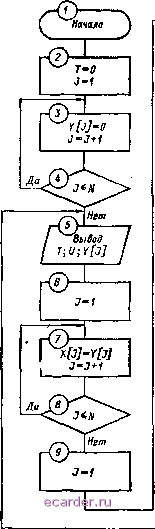 гт< > X[J]=Y[j]+f1[3j/2
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 [118] 119 120 121 122 123 124 125 126 127 128 129 130 |