Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 [36] 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130

мального момента при заданном токе статора. Такие задачи ynpailv ления решаются при использовании экстремальных систем управления.

3-3-2. СИСТЕМЫ ЧАСТОТНОГО УПРАВЛЕНИЯ С ФУНКЦИОНАЛЬНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ КООРДИНАТ

При частотном управлении асинхронным двигателем напряжение статора может в общем случае регулироваться как в функции относительной частоты статора v, так и в функции момента нагрузки. Прн этом предполагается, что абсолютное скольжение может определяться, а относительное напряжение статора 7 является функцией V и Sg, т. е. V = 7 iy а). Тогда, используя запись момента в общем виде, имеем

---ti-. SHiv, S,), (3-58)

где 1 (v, Sj) = R2SJA (v, S3).

Условие максимума момента определяется выражением = О, илн

2l{v, S,)v(v. S.)% + v4v, S,) = 0.

Из этого выражения нельзя получить ойцие формулы критического скольжения н критического (максимального) момента для произвольной зависимости v от v и S2. В частном случае, когда v ие зависит от Sg, например для постоянной нагрузки двигателя dv (V, S2)/dS2 = О, и

С учетом равенств (3-57) дМ

Отсюда значение критического абсолЕОГного скольжения

S. p = =bR;/+g. (3-59)

Подстановкой выражшия (3-59) в (3-58) находится значение критического момента

miUU 2- . (3-60)

/?iV±K(6* + cvS)(da+e*v )

На основании (3-60) записывается функциональная зависимость относительного напряжения у от относительной частоты v. Приравняв к единице отношение критических моментов при номинальной

и при любой другой частоте, т. е. Мкр/Лкр.н U получим

/ ДхУУСтаЖНу-) р (3.61)

Из выражения (3-61) следует, что для постоянства критического момента при уменьшении частоты необходимо уменьшать знаГение напряжения в меньшей степени, чем значение частоты. Графическое

представление у = F (v) показано на рис. 3-14, а [401. Вид механических характеристик двигателя при управлении частотой и напряжением статора в соответствии с условием (3-61) показан на рис. 3-14, б. Значения синхронных угловых скоростей Щ1> соа. (Ооз соответствуют трем произвольным значениям частоты напряжения статора.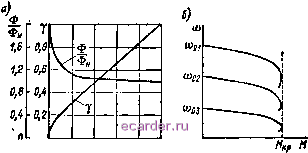

О 0,2 4 0.6 0,8 V

Рис. 3-14

Следует, однако, иметь в виду, что прн большом снижении частоты постоянство критического момента обеспечивается за счет увеличения магнитного потока двигагеля и соответственно тока намагничивания. Примерный график изменений относительного потока двигателя в зависимости от относительной частоты статора показан на рис. 3-14, а. Из графика следует, что постоянство потока двигателя обеспечивается прн снижении частоты до значений, составляюш.их примерно 0,2 - 0,3 номинального значения. При большем снижении частоты постоянство перегрузочной способности привода сопровождается резким увеличением потока двигателя и тока намагничивания. С учетом насыщения двигателя и ограничений по току статора получение критического момента прн значениях v<0,l, равного критическому моменту при v= 1 становится проблематичным.

Аналогично можно получить иные законы регулирования, например определить у - F (v) прн вентиляторной нагрузке привода при постоянстве мощности и др. Однако в каждом из этих случаев расчет у = f (v) необходимо производить для вполне определенной нагрузки двигателя. Произвольные изменения нагрузки в процессе регулирования скорости могут приводить к нарушению нормальных условий работы двигателя.

Реализуя желаемые зависимости у = F (v) с поммцью функциональных преобразователей в системах управления асинхронными короткозамкнутыми электродвигателями, можно получить простейшие схемы управления. На рис. 3-15, а показана разомкнутая система частотного управления. Напряжение с задатчика иитенсивностн (ЗИ) непосредственно поступает для задания частоты на вход автономного инвертора (ЛИ) и через функциональный преобразователь (ФП) для задания напряжения на вход управляе.мого выпрямителя (У5). В рассматриваемой системе применен ТП частоты со звеном постоянного тока. Аналогично выполняется система н с ТП частоты с непосредственной связью. В системе управления с ФП могут использоваться обратные связи по напряжению УВ нли всего ТП. На рис. 3-15, б показана функциональная схема системы с контуром регулирования напряжения УВ. На схеме обозначено: ДИ - датчик напряжения; РН - регулятор напряжения.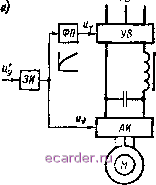

ЗИ -

Рнс. 3-15

Если регулировочные характеристики ТП частоты по каналам напряжения н частоты нелинейны, то в характеристике ФП требуемая завнснмость у ~ F (v) должна быть реализована с учетом &ТИХ нелинейностей. При прочих равных условиях зависимости у = F (v) в схемах рис. 3-15, а, б будут нескатько различаться, так как они рассчитываются в зависимости от параметров статориой цепн двнгателя совма:тно с приведенными сопротивлениями ТП частоты. Последние же в рассматриваемых схемах будут различны. В схеме рнс. 3-15, б производится стабилизация напряжения УВ, и тем самым уменьшается приведенное сопротивление статорной цепи. При использовании регуляторов напряжения с интегральной составляюш.ей (см, гл. 1) статическая ошибка контура регулирования Р1апряжения может быть принята равной нулю. Если использовать в системе управления обратную связь по выходному напряжению ТП частоты, то при расчете у f (у) можно учитывать только параметры статорной цепи двигателя.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 [36] 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130