
 | |
|
Слаботочка Книги 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 [39] 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 механических характеристик могут быть применены контуры регулирования скорости двигателя. Примером такой системы является система, функциональная схема которой показана на рис. 3-20, б. Входное напряжение ФЯ определяется как разностный сигнал между выходным сигналом регулятора скорости PC и сигнало.м тахогенератора Тг. Задание на скорость вводится через ЗИ на вход контура регулироваипя скорости двигателя. В системе управления имеются два взаимосвязанных контура регулирования, одни нз которых решает задачу приближенной стабилизации потока, другой обеспечивает требуемую жесткость механических характеристик. Схема системы частотно-токового управления, соответствующая функциональной схеме рис. 3-20, а, погазана на рнс. 3-21. Функциональный преобразователь реализуется на операционных усилителях / и 2, На усилителе 1 реализуется ограничение напряжения, а иа усилителе 2 и диодах Д1, Д2 - знакопостоянство выходного напряжения при знакопеременном входном напряжении. Стабилитрон Д5 и дополнительный сигнал /j.x на входе регулятора тока формируют нижнюю часть характеристики = F (Sg) и определяют ток статора в режиме холостого хода двигателя. Регулятор тока РТ принят пропорционально-интегральным. Формирование сигнала, пропорционального Sg, производится на усилителе / путем вычитания из сигнала задания сигнала с выхода делителя Тг. 3-3-5. СИСТЕМА ВЕКТОРНОГО УПРАВЛЕНИЯ Раздельное управление скоростью и потокосцеплением асинхронного короткозамкнутого электродвигателя можно эффективно производить, используя принцип векторного управления [14, 56Ь Координаты электропривода, измеренные в неподвижной системе координат, могут быть преобразованы к вращающейся системе координат, н из них могут быть выделены постоянные значения, пропорциональные составляющим векторов во вращающейся системе координат. По этим координатам и производится управление. Исходной информацией для построения системы векторного управления является информация о мгновенных значениях и пространственном положении вектора потокосцепления в воздушном зазоре, мгновенных значениях токов или напряжений статора и скорости ротора двигателя. Вращающаяся система координат принимается определенным образом орнеитированной относительно вектора потокосцепления двигателя. Удобнь(е алгоритмы управления имеют место прн ориентации координатной системы относительно вектора потокосцепления ротора. Функциональная схема системы векторного управления показана на рис. 3-22. Система имеет два канала управления: модулал вектора потокосцепления ротора и угловой скоростью ротора. Двухканальная система управлепия дает возможность осуществить независимое регулирование модуля вектора потокосцепления ро- тора и скорости ротора при сохранении прямой пропорцноиа.1ьно-сги между моментом. развиваемы\1 двигателем, и составляющей намагничивающей силы статора, находящейся в квадратуре с волной потокосцеплення ротора. орт 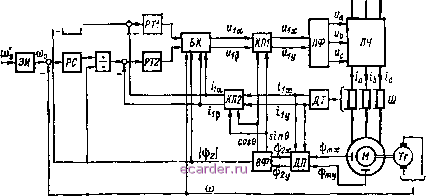 Рис 3 22 Измерение текущих значений переменных производится в неподвижной системе координат с помощью датчика потока (ДП) и датчика тока статора (ДТ). Датчик потока измеряет составляющие ipMx, twy в воздушном зазоре двигателя при помошл датчиков Холла, установленных в расточке статора по осям х - у, причем ось X совмещается с магнитной осью обмоткн фазы а. Кроме того, в ДП осущтвляется вычисление составляющих потокосцеплення ротора согласно формулам 2у - щ- Фту eifjiiyt где fea - коэффициент электромагнитной связи ротора, = LmJL-Эти формулы получены из уравнения ~ {} jk - -заи счедующего из уравнений = хЬ + 12-2 и if = (ij + (2). если результирующие векторы представить в внде проекций в неподвижной системе координат аналогично равенствам (3-14). ДТ измеряет мгновенные значения токов в трех фазах статора гю. hb> he и преобразует их в двухфазную систему переменных ilv) и/ Для пересчета переменных из неподвижной системы координат в систему координат, связанную с потокосцеплением ротора, ис-патьзуется вектор-фильтр {ВФ) и координатный преобразователь КП2. Вектор-фильтр осуществляет выделение модуля вектора потокосцеплення ротора I Фг I и тригонометрические функции cos 9 н sin 9, синфазные первым гармоническим составляющим -ф.- и Координатный преобразователь КП2 представляет собой мат-HV из четырех б.чоков произведения и осуществляет ортогональ-**ое преобразование - поворот вектора намагничивающей силы ста- 3 на >гол, равный мгновенной фазе вектора потокосцепления оотора в осях а - р относительно неподвижных осей х - у в соответствии с формулами, записанными через токи статора: - tlx cos е + kg sin б; \ Щ = - tlx sin е 4- cos е. J Уравнения переходных процессов в асинхронном двигателе при векторном управлении, выраженные в системе координат, ориентированной относительно вектора потокосцепления ротора, могут быть получены на основании уравнений {3-6). Подставив в уравнение < - Rlh + +/ К - 2, значение тока ротора пачучеиного на основании уравнения (3-8), и выполнив необходимые преобразования с учетом того, что для электродвигателя с ко-роткозамкнутым ротором 5 = 0, а Ь/Ц - k, получим - - + hRA - i (ш - Pn<i>) *з. (3-71) Подставив в уравнение значение потокосцепления статора и выполнив необходимые преобразования с учетом уравнений (3-70), (3-71), получим = - 5i±p- ii - ]ф,н + - /Рп {f Ъ + ТГ 1- (3-72) где по аналогии с (3-216) Li~~ {L%IU) + Ца. Выразив результирующие векторы через их вещественные и мни-е Части в соответствии с равенствами (3-14), а также учитывая формулы (3-69) ортогональных преобразований, можно записать Уравнения (3-71) и (3-72) в системе координат, вращающейся со скоростью й)к, равной угловой скорости вращения вектора потоко-Депления ротора wj , приведенной к двухполюсному электродвнга- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 [39] 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 |