|
| |
|
Слаботочка Книги
Axjt Рйс. 1-4 Дйната представрПяет собой произведение переменных Хг и Xg, Прн лнтеариза-ции, давая ирирашения переменным, можно записать Произведение .Угмач-нач войдет в уравнение статики и будет исключено из системы уравнений в приращениях. После исключения произведения ДхДх как величины второго порядка малости операция умножения окажется за\ге- ненной суммированием. В прямые каналы будут введены звенья с передаточными коэффициентами Анач н Хг нач значения которых определяются выбором режима, принятого за начальный (рис. 1-4), Линеаризация гладких нс1и-нейпых характеристик связей ссо-дитси к замене иел1шениой связи пропорциональным звеном с коэффициентом передачи, представляющим собой в о. е. тангенс угла наклона касательной к характеристике связи в точке, соответствующей начальному режиму, как это показано на рис. 1-3, б для коэффициента ki. В абсолютных единицах (а. е.) коэффициент передачи определяется как отношение приращений выходной величины к входной, определенных по касательной в рабочей точке (рис. 1-3, а). Коэффициенты в а. е. н о. е. связаиы меаду собой выражением Очевидно, что значения ft; и й; зависят от того, в какой рабочей точке работает система. При линеаризации нелинейной связи, охватывающей элементарное звено, в зависимости от рабочего режима различными оказываются и коэффициент передачи получающегося апериодическогозвена, и его постоянная времени. В точке Д (рис. J-3, б), где касательная к характеристике связи параллельна прямой, про-(Ходящей через начало координат и точку В, соответствующую базовому режиму, коэффициент обратной связи ka.c. кач - постоянная времени равна g. В другой рабочей точке о-с-пач отличен от единицы и апериодическое звено, на вход которого действуют сигналы АДС/, нач Дп гят A*jr описывается передаточной функцией 1/(Пйр) gft ГДе ft = 1/Йо.с.1шч; Tff = Уйб/Жо.с.нэч- Система управления может содержать и негладкие нелниейпостн, например, типа ограничения зоны нечувствительности в др. Прн анализе такой системы иногда удается выделить режимы, в которых эти нелинейности не оказывают влияния на ее работу. Так, например, ограничение выходного напряжения регулятора не сказывается при малых значениях входного сигнала, наличие сухого трения иногда может не учитываться, если в процессе регулирования скорость двигателя не снижается до значений, близких к нулю, не во всех режимах создаются условия, при которых в результате влияния зазора двигатель и ИО оказываются не связанными друг с другом, В этих случаях система может рассматриваться как линеаризованная. При исследовании режимов, в когорых исключить влияние нелинейности нельзя, широко применяется метод гармонической линеаризации в совокупности с расчетами на АВЛ\ н ЦВМ. 1-2-2. ФОРМЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ЛИНЕАРИЗОВАННЫХ АСУ ЭП После линеаризации основных нелннейностей могут быть записаны линейные дифференциальные уравнения, описывающие физические процессы в системе. Рассмотрим в качестве примера замкнутую АСУ ЭП, включающую в себя объект регулирования в виде интегрирующего звена с постоянной времени Т, на вход которого поступают напряжение с выхода источника питания Дып и возмущение d B03 - Ксйффицвен1Ы передачи объекта по каналам этих воздействий есть соответственно key и вози- Предположим, что источник питания может быть описан апериодическим звеном с коэффициентом передачи и малой постоянной времени Tji, а в качестве регулятора используетси усилитель с коэффициентом усиления kp. На входе усилителя сравниваются управля* ющий сигнал, пропорциональный предписанному значению регулируемой величины, приращение которого обозначим ДИу, и сигнал обратной связи, приращение которого есть Дыо.с feo. сД вых. Система уравнений, отвечающих физике явлений в описанном контуре, имеет вид 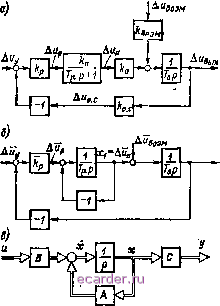 Рис. 1-5 A MV = Д п.с = о.1-ДУнЫУ. где р = d/di; Д р - приращение напряжения на выходе регулятора; Аиых - приращение регулируемой величины. Этим уравнениям соответствует структурная схема в а. е. на рис. 1-5, а. Состояние системы л-го порядка в любой момент времени может быть охарактеризовано положением в л-мерном пространстве состояний изображающей точки, координатами которой являются выходные переменные элементарных звеньев системы или их линейная комбинация, Такому представлению соответствует запись дифференциальных уравнений в нормальной форме. Для контура второго порядка, описываемого уравнениями (М). исключая переменные hup и Дно.с! производные от которых не фигурируют в описании системы, уравне- ВИЯ в нормальной форме можно записать как м- (1-2) С целью сокращения числа коэффициентов можно нормировать уравнения (1-1), приняв за базовое значение выходной координаты некоторое значение Оашк б и определив другие базовые значения как (/ ози.б fBwt б/воаи. f/n.6= = Свыч.б/о. fp.6~ fn tK, Uy.b- fo.c.6= feo-cftux 6.Введя, как это принято при записи уравнений в форме пространства состояние*, обозначения Дп - х, вых = . Рп = А> рД вых -2. уравнения, анало1Ичные (1-2), можно записать 8 виде -{-Xt-x + h Д у); (Х1-(~ДНвоз ), (1-3) . где Д у = AuvWy.e< ASeow = Д чозм-во1м.б; = ру б/Ер.б. Уравнениям (1-3) соответствует нормированная детализированная структурная схема рис. 1-5,6, содержащая в своел! составе интегрирующие звенья (Тор) и 1/(Tjjp) и звено с безразмерным коэффициентом регулятора йр. Такая структурная схема удобна при структурном моделировании с помощью АВМ, так как факгически является уже готовой наборной схемой модели. Уравнения (J-2) и (1-3) позволяют ввести в рассмотрение векторы и матрицы, что оказывается особенно цечесообразным при исследовании сложных систем с помощью ЦВМ При этш состояние системы представляется вектором х в л-мерном Пространстве состояний, а т внешних входных воздействий образуют вектор U в пространстве размерности т. В реальной системе не все переменные состояния могут быть измерены для того, например, чтобы осуществить по ним замыкание системы. Поэтииу вводится понятие измеряемых переменных. Пусть таких переменных г и они составляют вектор измеряемых переменных у, Система уравнений, описывающих динамику системы управления, может быть записана в следующей компактной форме: x = Ax4-Bu; У=Сх, (1-4) где А - (п X п)-матрица коэффициентов; В - (п X п)-чатрица управленпя; С - (г X гг)-матрица выходного сигнала. Такой записи соответствует матричная структурная схема рис. 1-5, в, на которой символ 1/р означает операцию интегрирования. Для рассматриваемого примера можно записать, предполагая, что измеряемой координатой является только ух; U- Дд Лй в отличие от структурных схем рис. 1-5, а, б матричная структурная схема яесет необходимую информацию о системе лишь сошиестно с выражениями для матриц А, В и С. Ее удобно использовать, в первую очередь, при рассмотрении сложных н нногосвязных структур. 1 2 3 [4] 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 |
|||||||||||||||||||||||||||||