Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 [50] 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130
https://dostavka-byketov.ru Доставка цветов по Клину.

приходится выбирать на октаву левее этой частоты. Переходная характеристика в системе с ЯЯ-регулятором для случая у = 5,8

при 7ц, = 0, Pp.. = Vo, Tp.c = 2/w,poi показана иа рис. 4-9 штриховой линией.

Поскольку переходный процесс, соответствующий настройке на ОМ, принято считать наилучшим, можно прн 7 > 5,8 и Tj о

рекомендовать выбирать ftp. с так, чтобы коэффициент демпфирования составлял Eg = К2/2, т. е. чтобы рабочая точка располагалась на линии равного значения 1 = Y2/2 = const. Этого можно достичь и при умень-шении ftpc по сравнению с (Л < В), и прн увеличении его {Л > В). В первом случае переходный процесс будет более длительным, чем при Ар = = fep.co- Поэтому практический интерес представляет второй случай (кривая бг на рнс. 4-8). Зная 7, можно определить А н В на пересечении кривых бг\\у~ = const и на основании одного из выражений (4-15) определить требуемое значение ftp,.. Прн таком выборе ftp.c чем выше у, тем больше %i по сравнению с Хх н тем ближе переходная характеристика A<ajM.y к кривой второго порядка при коэффициенте демпфирования 12/2.

Практическая возможность реализации описанных настроек зависит от справедливости предположения о том, что малые постоянные времени в контуре скорости реально малы. Если прн выборе коэффициента регулятора скорости равным ftp . суммарная малая постоянная времени коитура скорости будет удовлетворять условию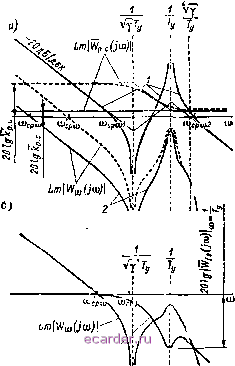

Рис. 4-10

;о,5Гу/р>,

(4-21)

т. е. соответствующая ей частота будет хотя бы в два раза больше, чем и.риа (рис. 4-10, а), то запас по фазе при частоте (Лср.(л2 = VV/ будет близок к 60 и зауыкаиие системы с ft = ko будет воз-

.можно без значительного увеличения колебательности контура ско-

Поскольку в жесткой системе со стандартной настройкой быстродействие зависит только от значения Txa, а в системе с упругостью определяется Ту, иеобходимость выполнения неравенства (4-21) указывает на то, что прн реализации рассматриваемой настройки быстродействие линейной упругой системы по сравнению с быстродействием жесткой будет тем хуже, чем больше v- При увеличении по сравнению со значением, определяемым выражением (4-21), будет увеличиваться колебательность контура скорости на частоте, близкой к \/Ту.

При v > 5,8 и выборе рабочей точки на кривой бе ЛАЧХ Lm I Wtp (/<й) I пойдет выше характеристики, соответствующей k с р.со. частота риа возрастет н требования к допустимому значению будут более жесткими.

Если суммарная малая постоянная времени недопустимо велика, реализовать рассмотренную настройку оказывается невозможным из-за неустойчивости контура скорости. Тогда коэффициент усиления PC придется снизить так, чтобы резонансный всплеск ЛАЧХ при частоте 1/Ту лежал ниже оси частот (характеристика 2 на рнс. 4-10). Естественно, что при рассмотрении этого случая нельзя пренебрегать механическим демпфированием. Быстродействие системы в этом случае будет определяться частотой среза срщ, которая значительно ниже частоты шриа и частоты Qq, определявшей быстродействие системы прн - 0.

При значениях 7 > 10 20 быстродействие системы может быть повышено по сравненрю с тем, которое соответствует характеристике 2 иа рис. 4-10, за счет применения PC с передаточной функцией

ЩАР) = К.гГ ( -22)

Высокочастотная часть ЛАЧХ этой функции проходит на высоте 20 1gfep, где значение ftp соответствует характеристике 2. На рис. 4-10, а показана характеристика Lm ] (/&)) j при

fpciV Туи Тр,с2 = у- Быстродействие в этом случае определяется частотой среза (йри и повышается примерно в у раз по сравнению с быстродействием системы, в которой использован пропорциональный PC.

Выше предполагалось, что при частоте 1/Ту вследствие высокого быстродействия и отсутствия влияния обратной связи по ЭДС двигателя амплитуда частотной характеристики замкнутого контура тока (/о ) jy-i равна единице. Если иа самом деле

ЛАчХ замкнутого контура тока имеет на этой частоте провал, то также может позволить увеличить частоту среза контура ско~ рости по сравнению с Исрш- Поэтому иногда рекомендуется специально снижать быстродействие контура тока, как показано

на рис. 4-10, б, где частота среза токового конгураснижена до значения ор/, близкого к 1/(/7у). Поскольку при пропорциональном PC передаточная функция разомкнутого контура скорости имеет внд

уменьшение быстродействия токового контура снижает резонансный всплеск ЛАЧХ разомкнутого контура скорости на 20\g\Wis{i(a)\fary позволяя, так же как при применении регулятора с передаточной функцией (4-22), увеличить быстродействие.

Во избежание низкочастотных колебаний в системе не следует делать Иср/ меньше, чем (1,5 2)о)сри (рис. 4-10, б). Недостатком этого способа коррекции является ухудшение качества ограничения тока якоря н увеличение сшибки системы при изменении напряжения сети,

4-2-3. НЕКОТОРЫЕ СПОСОБЫ КОРРЕКЦИИ СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ С УПРУГОСТЬЮ ПРИ МАЛЫХ КОЭФФИЦИЕНТАХ

СООТНОШЕНИЯ МАСС

При значениях -у <: 1,5 ч- 2,0 добиться эффективного демпфирования упругих колебаний скорости ИО без значительного снижения быстродействия только за счет выбора структуры и параметров PC невозможно. Методы коррекции таких систем связаны с применением тех или иных корректирующих связей по скорости механизма.

Одни из наиболее эффективных способов заключается во введении на вход системы сигнала по производной от скорости ИО. Чтобы оценить принципиальные возможности рассматриваемого способа коррекции, обратимся снова к системе без малых постоянных времени, считая, что осуществляется идеальное дифференцирование. Положим в схеме рис. 4-7 Wo.ci (р) = Т-р, \io.c2 ip) Аналогично выражениям (4-13) и (4-20) можно получить

А<Ва (jp) 1

-fr-hynp+ii+nJ.pi

D.C \ p.t /

Коэффициенты Вышнегр аде кого записываются в виде

(4-23)

уу V; v-p- tJV 7-ySp,

откуда == V ( + р.с T.,ilTJ. 154

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 [50] 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130