Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 [65] 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83

При проверке соотношения (94) также необходимо учитывать влияние магнитной текстуры и парапроцесса.

Теоретическая сторона вопроса о влиянии на четные явления объемных эффектов была рассмотрена в работе Акулова [11] и более подробно в работах Симоненко [12] и Вонсовского [13].

§ 3. Гальваномагнитный и термомагнитный эффекты в области вращения и смещения

В предыдущем параграфе мы имели дело с величинами гальвано- и термомагнитных эффектов при намагничении до насыщения и рассматривали, как они изменяются при повороте результирующего вектора 4 в ферромагнитном металле. Пусть теперь ферромагнитный металл помещен в магнитное поле, меньшее, чем поле насыщения (Я<Яз). Величины возникающих при этом изменений электропроводности и термоэлектродвижущей силы можно было бы определить, если бы была известна функция распределения 4 областей, соответствующая намагниченности I < 4, создаваемой полем Я.

Используя закон анизотропии и методы статистической физики, Акулову [3] удалось найти такую функцию для случая намагничивания никеля и железа в слабых полях. Она позволила объяснить поведение гальвано- и термомагнитных эффектов в полях, где процесс намагничения происходит путем смещения. Из этой теории следует, что указанные эффекты должны иметь квадратичную зависимость от намаг-ниченнссти как в монокристаллических, так и поликристаллических образцах никеля и железа.

На рис. 100 и 101 приведены результаты измерений термомагнитного эффекта в поликристаллическом никеле по работе Волкова [14] и гальваномагнитного эффекта для железа по работе Феденева [15]. На рис. 100 по оси ординат отложены величины изменений термоэлектродвижущей силы в магнитном поле, отнесенные к градиенту температуры в исследуемом образце, а на рис. 101-относительное изменение электросопротивления образца при включении поля. Из этих данных видно, что в согласии с теоретическими выводами в слабых Г10ЛЯХ оба эффекта линейно здвцсят от Р. При некртором

поле, которому соответствует при намагничивании смена процесса смещения процессом вращения, имеет место резкий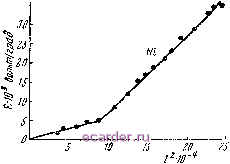

Рис. 100. Зависимость термомагнитного эффекта никеля от квадрата намагниченности.

излом прямой. Этот излом наблюдается только у хорошо отожженных материалов; в случае наличия в металле неоднородных напряжений область, в которой происходит смена смещения вращением, размазывается на более щирокий интервал полей, и резкого излома не наблюдается.

Из рис. 100 и 101 видно, что в области смшцеиия гальвано- и термомагнитные эффекты растут менее интенсивно, чем в области вращения. Для объяснения этого факта нужно принять во внимание следующее. В слабых полях рост намагниченности происходит за счет двух процессов: переориентации /g областей на 180 (смещение границ между областями С антипараллельными векторами /g) и изменения направлений

V 8 12 /6

Рис. 101. Зависимость гальваномагнитного эффекта железа от квадрата намагниченности.

Ig областей на угол, меньший, чем 180° (смещение границ между областями, моменты которых находятся под углом, отличным от 180°). Первый процесс в силу четности гальвано-и термомагнитных эффектов не дает изменения электросопротивления и термоэлектродвижущей силы и, следовательно, последние в основном изменяются здесь за счет второго процесса. В зависимости от того, какую долю в намагничении ферромагнетика составляют ориентации Ig областей на 180° и на угол, меньший, чем 180 мы можем получить малые или большие величины изменения электросопротивления и термоэлектродвижущей силы на участках кривых, где происходит смещение (до точки излома кривых, приведенных на рис. 100 и 101). Эти участки на кривых гальвано- и термомагнитных эффектов можно искусственно совсем уничтожить , если создать в ферромагнетике механические деформации, затрудняющие или вовсе исключающие процесс смещения. Такие условия можно обеспечить в поликристаллическом никеле, если его сильно растянуть внешними нагрузками. На рис. 102 приведена кривая термомагнитного эффекта для такого образца в функции квадрата намагниченности [14]. Кривая показывает, что при возрастании упругого растяжения участок кривой, соответствующий смещению, съедается , и, начиная с некоторого значения упругого растяжения, термомагнитный эффект целиком определяется процессом вращения. Аналогичные кривые были получены и при измерениях гальваномагнитного эффекта никеля [15]. Следует отметить, что здесь опыт дает, как и в случае магнитострикции (см. гл. II, § 3), линейную зависимость гальвано- и термомагнитного эффектов от квадрата намагниченности (рис. 102).

В других материалах с помощью упругих напряжений можно создать в ферромагнитном металле такие условия,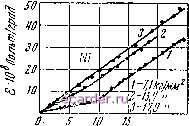

140-

Рис. 102. Влияние упругих растяжений на термомагнитный эффект никеля.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 [65] 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83