Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 [79] 80 81 82 83

Далее, так как

имеем:

Это соотношение показывает, что при адиабатическом изменении магнитного состояния ферромагнитного тела, вызванного наложением поля Н, температура его меняется.

Пользуясь термодинамикой, мы можем также получить соотношение (111) в форме

dT-dlg. (112)

Это выражение показывает, что dT непосредственнр связано с изменением величины самопроизвольной намагниченности dig.

Из формулы (111) видно, что dT в области парапроцесса имеет всегда положительный знак, ибо для всех ферромагнетиков величина отрицательная. При приближении

определены таким же способом, как и обратимые тепловые эффекты за счет вращения (см. § 2), т. е. дифференцированием свободной магнитной энергии ферромагнетика и приравниванием получающегося результата выражению для энтропии. Изменение свободной магнитной энергии при парапроцессе равно

dF = HdIg,

где dig - приращение величины самопроизвольной намагниченности. Дифференцируя по Т, найдем энтропию, соответствующую этой энергии: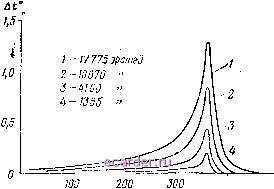

4Q0 t°C

Рис. 134. Температурная зависимость магнетокалорического эффекта в никеле (обратимые изменения температуры при парапроцессе).

разим через /g. Воспользуемся уравнением мапштного состояния Вейсса (см. гл. I § 2):

А = 1(Мз--Я). При одновременном изменении 4, Я и Г имеем:

Отсюда при / = const, найдем:

К точке Кюри, где -; быстро растет, магнетокалорический

эффект должен достигать особенно больших величин. На рис. 134 дана по измерениям Вейсса и Форера [6] температурная зависимость магнетокалорического эффекта никеля. Видно, что в точке Кюри эта величина эффекта достигает максимума, а при удалении от нее быстро уменьшав!ся.

Найдем зависимость магнетокалорического эффекта от самопроизвольной намагниченности, для чего в (112) вы-

Подставляя (113) в (112), получаем;

dT=-{HNI,) dig,

где Я <: Nig.

Интегрируя последнее выражение, мы окончательно найдем:

(114)

где а - числовой коэффициент, в который входит постоянная молекулярного поля (или, что то же, величина обменного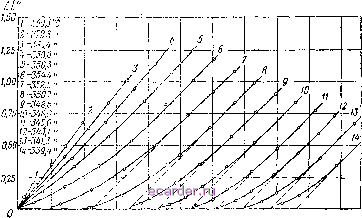

ЮО 150 200 250.J 2 300 3S0 tOO 4У0 SOO

Рпс. 135. Кривая магнетокалорического эффекта никеля в функции квадрата намагниченности.

интеграла). Таким образом, здесь, как и для других ферромагнитных явлений (магнитострикции, гальваномагнитного эффекта и пр.), в области парапроцесса должно быть справедливо правило пропорциональности величины эффекта квадрату самопроизвольной намагниченности. Это подтверждается результатами экспериментальных исследований. На рис. 135

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 [79] 80 81 82 83