Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 [26] 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104

3 4. ОДНОФАЗНАЯ МОСТОВАЯ СХЕМА

Двухполупериодное вып ствлено также при помощи выпрямления, приведенной

Выпрямитель содержит и трансформатор Тр. В отличие от ранее рассмотренных схема является двухтактной, так как ток во вторичной обмотке протекает как в положительную, так и отрицательную части периода.

Рассмотрим работу схемы при питании от сети синусоидального напряжения.

На рис. 3-9,а показана форма напряжения на зажимах вторичной обмотки 2-

В первый полупериод, когда потенциал точки а (рис. 3-8) положителен, а потенциал точки б отрицателен, ток проходит через вентиль Ви нагрузку /? и вентиль fig в направлении, указанном сплошными стрелками. Вентили fia и fi4 в это время не пропускают тока

рямление может быть осуще-однофазной мостовой схемы на рис. 3-8.

четыре вентиля fii, В2, fia, fi4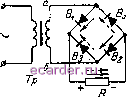

Рис. 3-8. Однофазная мостовая схема выпрямления.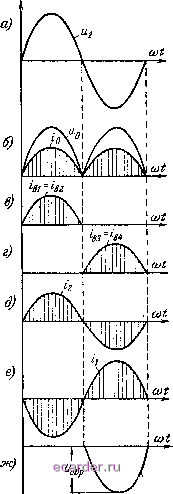

Рис. 3-9. Диаграммы напряжений и токов в однофазной мостовой схеме.

и находятся под обратным напряжением. В следующий полупериод, когда потенциал точки б становится положительным, а точки а - отрицательным, ток течет через вентиль Вз, нагрузку R и вентиль в4 в направлении, указанном пунктирными стрелками. Вентили В] и Вг в это время не пропускают тока и находятся под обратным напряжением.

Из рис. 3-8 видно, что направления токов, текущих через нагрузку в течение обоих полупериодов, совпадают. Поэтому, как и в схеме со средней точкой, в рассматриваемой схеме имеет место двухполупериодное выпрямление. На рис. 3-9,6 приведены кривые выпрямленного тока iu и напряжения о. Так как падение напряжения в обмотке трансформатора и в вентилях принято равным нулю, то форма выпрямленного напряжения повторяет форму напряжения на зажимах вторичной обмотки.

На рис. 3-9,6 и г приведены диаграммы токов через вентили В], Вг и в3, в4. Ток во вторичной обмотке трансформатора протекает в течение обоих полупериодов и является синусоидальным (рис. 3-9,(9), поэтому вынужденное намагничивание сердечника отсутствует. Ток в первичной обмотке также является синусоидальным (рис. 3-9,е).

На рис. 3-9,ж приведена форма напряжения между электродами вентилей В] и Вг. В течение второго полупериода, когда работают вентили Вз и в4, анод вентиля Вг, соединенный с точкой б вторичной обмотки, находится под отрицательным потенциалом. В это же время катод вентиля Вг имеет положительный потенциал, равный потенциалу точки а вторичной обмотки (так как падение напряжения в вентиле в4 при прямом токе равно нулю). Таким образом, в течение первого полупериода вентиль Вг находится под обратным напряжением, равным разности потенциалов между концами вторичной обмотки трансформатора. Максимальное значение этой разности потенциалов равно амплитудному значению напряжения вторичной обмотки. Нетрудно видеть, что закон изменения обратного напряжения на вентиле В] такой же, как и на вентиле Вг.

В течение первого полупериода разность потенциалов между электродами вентилей Bi и Вг равна нулю, а вентили Вз и в4 находятся под обратным напряжением та-

кой же величины, как вентили Si и Вг в предыдущий полупериод.

Переходим к выводу основных соотношений.

1. Определение величины действующего напряжения вторичной обмотки

Так как выпрямленное напряжение в рассматриваемой схеме имеет такую же форму, как и в схеме со средней точкой, то для определения действующего напряжения вторичной обмотки можно воспользоваться выведенным выше выражением (3-27).

2. Определение действующего значения тока вторичной обмотки

Действующее значение тока /г находим, пользуясь выражением (3-7). В отличие от предыдущих схем интегрирование производим в пределах от О до 2я:; тогда имеем:

- 5 амакс

Vo о

Подставляя значение /амакс из (3-28) в (3-45), получим:

(3-46)

/ -- =1 11/

3. Определение действующего значения тока первичной обмотки

Ток первичной обмотки находим по формуле (3-33), выведенной для схемы со средней точкой. Формула эта справедлива и для мостовой схемы, так как в обоих случаях по обмотке протекает синусоидальный ток.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 [26] 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104