|
| |
|
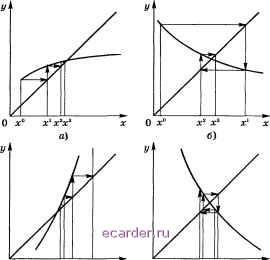Слаботочка Книги  в) г) Рис. 7.1.1 Нахождение каждого нового значения х~ требует решения, вообще говоря, нелинейного уравнения с одним неизвестным. Промежуточное место между итерационными методами (2) и (7) занимает метод, где компоненты приближений определяются из соотношений 1 - . +1 - .п+1 .п 3-2 - 92(Xi ,Х2,...,Хт), Хт - Ут(Х1 Х 1, Х). Методы (7) и (8) особенно широко использовались в различных моделирующих устройствах, так как они требуют малого объема памяти и просты в реализации. В достаточно малой окрестности решения X системы для приближений методом простой итерации имеем X = g(x ) - g(X) В(х - X), (9) Таким образом, при приближениях, находящихся в малой окрестности решения, погрешности приближений итерационного процесса (2) (а также и процессов (7) и (8)) подчиняются примерно тем же законам, что и погрешности итерационных методов решения систем линейных уравнений. Наличие соотношения (9) позволяет производить ускорение сходимости итерационных процессов. Рассмотрим случай m = 1 и построим аналог й-процесса. При имеющемся приближении ж обозначим ж = /(ж ), ж = д{х ). Согласно (9) ж -Х (7(Х)(ж -Х), ж 2-Х (7(Х)(ж - X). Из этих соотношений получаем д\Х) у.П ж 2 - (?(Х)ж 1 ~ - Ж - - (ж )
1-<?() J ж 2-ж ж 2 - 2ж 1-Ь Ж За следующее после ж приближение примем а;гг2 2а;п1 -I- ж </(<7(ж )) - 2<?(ж ) -Ь ж (10) Для характеристики методов решения уравнений вводится понятие порядка метода. Говорят, что метод имеет к-й порядок, если существуют Ci > О, С2 < оо такие, что р(х +,Х)С2(р(х ,Х))= при условии /э(х , X) ci. Чем больше к, тем быстрее сходится процесс итераций при малых значениях р(х , X), но каждая итерация метода при этом более трудоемка. В связи с этим в вычислительной практике наиболее распространены методы первого и второго порядков (например, метод, определяемый формулой (10), или метод Ньютона, рассматриваемый в следующем параграфе). Примечание. Иногда в литературе встречается другое, на наш взгляд неразумное, определение порядка метода: говорят, что метод решения системы уравнений F(x) = О имеет порядок к, если при его реализации вычисляются производные функций fi до порядка А; - 1 включительно. § 2. Метод Ньютона решения нелинейных уравнений Если известно достаточно хорошее начальное приближение к решению системы уравнений F(x) = О, (1) то эффективным методом повышения точности является метод Ньютона. Идея метода Ньютона заключается в том, что в окрестности имеющегося приближения х задача заменяется некоторой вспомогательной линейной задачей. Последняя задача выбирается так, чтобы погрешность замены имела более высокий порядок малости, чем первый (в определяемом далее смысле), в окрестности имеющегося приближения. За следующее приближение принимается решение этой вспомогательной задачи. Рассмотрим случай скалярного уравнетшя /(ж) = 0. В качестве такой вспомогательной задачи естественно взять линейную задачу /(х ) + /(.т )(.х-х ) =0. Ее решение х = Хп~f{xn)/f{xn) принимается за следующее приближение Хп+\ к решению исходного уравнения, т.е. итерации ведутся по формуле Хп+\ = Хп - f{Xn)lf{Xn). Рассмотрим более общий случай - решение нелинейного функционального уравнения. Пусть F(x) - оператор, отображающий линейное нормированное пространство Н на линейное нормированное пространство У, может быть и совпадающее с Н. Нормы в этих пространствах соответственно обознача- В § 6.10 были рассмотрены итерационные методы решения линейных систем с помощью спектрально-эквивалентных операторов. Аналогичные методы применяются и для решения нелинейных систем. Выбирается оператор G(x) такой, что х = О является единственным решением уравнения G(x) = 0. Приближения х + к решению системы F(x) = О определяются из соотношения G(x +i - х ) = F(x ). (11) Наиболее распространен случай, когда G - линейный оператор. В ряде случаев оператор G выбирается зависящим от п, а также от приближения х . Тогда в схему (11) укладывается также рассматриваемый ниже метод Ньютона решения нелинейных уравнений. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 [108] 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 |