|
| |
|
Слаботочка Книги Например, в случае, изображенном на рис. 7.2.2, все четные приближения совпадают с , а нечетнью -с Ь; метод, как говорят, зациклился . Для более сложных задач реальное поведение приближений ж при плохом начальном приближении становится суш;ественно более запутанным и трудно поддающимся анализу. Сравним асимптотическую скорость сходимости методов Ньютона и простой итерации. Для последнего мы имели оценку погрешности Цх-ХЦдЦх-ХЦ, д<1. Чтобы погрешность стала меньше е, согласно этой оценке достаточно взять Цх-ХЦ , 1 п log-i----log-i -. В случае метода Ньютона правая часть (7) будет меньше е, если > - log2 log2(cx -X bg2(ce) Таким образом, асимптотически, при е меньшего числа итераций. log2log2 -. (10) О, метод Ньютона требует Задача 1. Доказать, что для метода А;-го порядка. А; > 1, при наличии достаточно хорошего начального приближения число итераций, требуемое для достижения точности е, будет та ~ log log log А;. Обратим внимание, что метод Ньютона, записанный в форме (4), сам является разновидностью метода простой итерации. В случае скалярного уравнения /(ж) = О хорошо видна еще одна особенность метода Ньютона. Производная правой части (9) д{х) = х - f{x)/f{x) по х равна /(ж)/ (ж)/(/(ж)). Таким образом, р(Х) = О, если f{X) 7 О, и рис. 7.1.1 в этом случае приобретает следующий вид (рис. 7.2.3) Метод Ньютона оказывается удобным способом извлечения корней целой степени. Задача извлечения корня р - целое число, равносильна задаче решения уравнений - а = 0. Расчетная формула метода Ньютона в этом случае приобретает вид р - 1 а Хп+1 = -Хп + 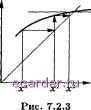 Задача 2. Рассматривается алгоритм вычисления у/а при 1 а 4, хо полагается равным значению многочлена наилучшего равномерного при- ближения для у/а на [1, 4] : жо = = + - Убедиться в справед- ливости неравенства ж4 - л/а\ 0,5 10 . В случае решения одного скалярного уравнения /(ж) = О наряду с методом Ньютона употребителен метод секущих. Простейший вариант этого метода заключается в следуюгцем. В процессе итераций фиксируется некоторая точка ж . Приближение .7, + находится как абсцисса точки пересеюния прямой, проходягцей через точки (жо, fix )) и (ж , /(ж )), с осью ж (рис. 7.2.4). Более эффективен способ, где за .г + принимается абсцисса точки пересечения с осью х прямой, проходяш,ей через точки (.т ~,/(ж )) и (.т ,/(ж )) (рис. 7.2.5). Уравнение этой прямой уп(ж)/(ж )+(ж-ж-);;2:1!Р- Из условия ?/,г(з; +) = о получаем ,п1 ,п fixm--x-) - ~ /(ж )-/(ж-1) Вычисления прекращают, когда одна из величин [ж * - ж или [/(ж ) -/(.т ) становится меньше некоторого заранее заданного малого > 0. Для достижения точности е этим методом, как и в случае метода Ньютона, при достаточно хороших начальных приближениях требуется 0(1п1п(1/е)) итераций. При решении системы т уравнений F(x) = О одним из возможных обобгцений метода секуш,их является следуюш;ий метод. Пусть определены приближения х ~ \ ..., х и известны значения Л(х -),...,/Дх ). Пусть у = Z/j(x)- уравнение плоскости. проходяш;ей через точки (x -,/i(x -)),..., (х ,/Дх )); за следующее приближение х + принимаем решение системы уравнений Li{x) =0, г = 1,..., ттг. При больших п эти плоскости становятся практически параллельными. Поэтому для т > 1 этот метод применяется редко, oбышo в случае, когда можно ограничиться невысокой точностью.  Рис. 7.2.4  В последнее время появились более совершенные обобщения метода секущих. Дело в том, что для этого метода при п сю характерно сплющивание т-мерного тетраэдра с вершинами в точках х ,..., х . Следствием этого является быстрое ухудшение обусловленности системы уравнений ii(x) = 0. В результате алгоритм вычисления становится неустойчивым к вычислительной погрешности и часто перестает сходиться. Кроме описанных выше, существует большое число других методов подобного типа, где в окрестности корня функция /(.т) приближается некоторой функцией д{х), для которой уравнение д{х) = О решается в явном виде. Однако для применения всех этих методов необходимо достаточно хорошее приближение к решению. Иногда для его определения используется метод вилки. Определяют со, Ьо такие, что /(ао)/(Ьо) < 0; выбирают каким-либо образом точку Со € (оО) о)) например берут Со = ( о + Ьо)/2 или за со берут точку пересечения секущей, проходящей через точки (со, f{ao)), (Ьо, /(&о)), с осью х. После вычисления /(со) за [oi, Ьх] принимают тот из отрезков [cq, cq], [cq, Ьо], на концах которого f(x) принимает противоположные знаки, и т.д. Важной задачей является разработка эффективных методов решения уравнений отдельных типичных классов. Для нахождения корней многочлена P{z) = ао2г Ч-----Ьото как с действительными, так и с комплексными коэффициентами таким методом является метод парабол. При заданных приближениях к корню Zn-2, Zji-i, Zji приближение Zn+i определяется следуюпщм образом. Строится интерполяционный многочлен второй степени, совпадающий с P{z) в точках Zn 2, Zn- За z+i принимается корень этого многочлена, наиболее близкий к z. В стандартных программах метода парабол эта схема подвергнута некоторой модификации. § 3. Методы спуска Для решения задачи минимизации функционала наиболее часто применяются методы спуска. При заданном приближении определяется какое-либо направление, в котором функционал убывает, и производится перемещение приближения в этом направлении. Если величина перемещения 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 [110] 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 |