Слаботочка Книги

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 [111] 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208

g 3. Методы спуска

взята не очень большой, то значение функционала обязательно уменьшится.

Рассмотрим примеры методов спуска.

При исследовании сходимости метода Зейделя в случае системы уравнений Ах. = b при А > О мы описали циклический метод покоординатного спуска минимизации функции Ф(ж1,..., Хщ) при заданном приближении Ф(ж5,..., ж) отыскивается значение xi = х\, нри котором достигается inf Ф(ж1, .Т2,..., ж[г), затем отыскивается значение х = Х2, при

котором достигается inf Ф(ж}, жг, ж3,..., .tJ), и т.д. Процесс циклически повторяется.

Обозначим через PkX приближение, получаемое при спуске из х по координате х. Присваивая приближению, получаюгцемуся при спуске по очередной координате, следуюпщй номер, можно записать приближения метода циклического покоординатного спуска в виде

х = Pix°, х = РгАх,...,

х- = Р г... Pix, Х-+1 = PiPm . . . PlX°, . . .

При практической реализации этого метода возникает проблема минимизации функций одной переменной. Рассмотрим отдельно задачу минимизации функций одной переменной Ф(.т) при начальном приближении к точке минимума ж = ж . Так как эта задача обычно не может быть решена точно, то часто поступают следующим образом: берут некоторые значения ж°, ж , и строят параболу у = Q2{x), удовлетворяющую условиям

д2(ж°) = Ф(жО), д2(ж°) = Ф(ж°), дгС ) = Ф(П

Абсциссу ж точки минимума гСж) принимают за следующее приближение ж. Уже в одномерном случае можно построить пример, когда последовательность точек, получаемых по описываемому методу, не обязательно сходится к искомой точке экстремума функции Ф(ж).

Даже если на каждом шаге отыскивается абсолютный экстремум функции Ф(ж1,..., а; г) но соответствующей координате, то уже при т = 2 может случиться, что итерационный процесс сходится не к искомой точке абсолютного экстремума, а к некоторой точке локального экстремума. На рис. 7.3.1 изображены линии Уровня такой функции и получаемые приближения. Спуск в циклическом порядке необязателен. Если из рассмотрения проводившихся ранее вычислений видно, что спуск по каким-либо координатам обеспе-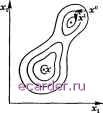

Рис. 7.3.1

чивает наибольшее убывание Ф(ж), то иногда целесообразен более частый спуск по этим координатам.

В других случаях при каждом п после получения приближения з; выбирается некоторая совокупность координат

производятся независимые спуски по координатам этой группы исходя из приближения х , т.е. находят точки Р,;( д)х . Далее вычпсляется

min Ф(Р;( мх ),

и соответствующая минимуму точка Рцп.к) принимается за х +.

Иногда номер очередной координаты, по которой осуществляется спуск, выбирается недетерминированно. В этом случае говорят о случайном покоординатном спуске.

Другой вариант метода спуска-метод наискорейшего [градиентного) спуска.. Следующее приближение отыскивается в виде

x-u+i =x -<5 grad#(x )

(рис. 7.3.2). Значение определяется из условия

min Ф(х - Sn grad Ф(х )),

т.е. этот алгоритм опять состоит в последовательной минимизации с]зунк-ции одной переменной

Как и в методе покоординатного спуска, в методе наискорейшего спуска нет необходимости полного решения вспомогательной задачи минимизации с]зункции одной переменной. В окрестности точки своего минимума эта с]зункция меняется мало, и тщательное нахождение ее точки минимума не приводит к существенному эффекту. В олучае метода наискорейшего спуска вопрос об объеме вычислений при минимизации вспомогательных функ-Рис. 7.3.2 ций одной переменной должен решаться

также с учетом относительной трудоемкости вычисления значений функции Ф(ж) и ее градиента.

Для иллюстрации решения вопроса о выборе метода рассмотрим следующую типичную задачу: решается нелинейная краевая задача для системы обыкновенных дис]зференциальных уравнений. В гл. 9 будет показано, что эта задача сводится к решению нелинейной системы уравнений F(x) = 0:

/i(x) = fi{xi,Хщ) = 0, г = 1,..., ттг.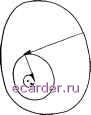

dfijxi,..., Хт)

fi{xi, Xj-i, Xj + A, Xj+i, X ,) - fi{xi, Xj, Xni)

Область сходимости метода Ньютона обычно невелика, поэтому по крайней мере на начальном этапе итераций целесообразно свести решение этой задачи к минимизации некоторого функционала и щзименить какой-либо из методов спуска. Рассмотрим простейший случай функционала

Ф(х) = 5;(AJ,:(x))2;

множители Ai = const Ф О, называемые масштабными, подбираются из условий конкретной задачи.

Пусть х = (ж ,a; j)-полученное приближение и решено сделать спуск в направлении А = (Ai,..., Am), ЦАЦ = 1. Вычисляют приближенные значения производных в этом направлении:

i = (/i(x + eA)-/,(x ))/e. (2)

На прямой X = х -f tA имеем

/i(x) /i(x ) + tk,

поэтому следующее приближение х + = х -Ь iA определяют из условия

minJ](Ai(/i(x )-biZ,;)) .

Отметим, что в данном случае существен вопрос о разумном выборе е в формуле (2). (По этому поводу см. § 2.16.)

Задача минимизации функции при наличии ограничений, так называемая задача условной минимизации, формулируется следующим образом. Ищется величина

А= inf Ф(ж1,..., ж) (3)

Xl,...,Xm

обладающей следующими свойствами.

Количество операций при отьюкании одного значения /Дх) и при одновременном отыскании всех значений /г(х), г = 1,..., ттг, в той же точке одинаково; обозначим его через А. Количество операций при непосредственном отыскании значений 5/,:(x)/S.Tj и нри одновременном отыскании всех значений dfi{-x.)/dxj, г = 1,..., тп, в той же точке одинаково. Обозначим его через В\ обычно jB 2> Л.

Тогда при решении задачи методом Ньютона целесообразно вычислять производные dfi{x.)/dxj, j = 1,..., m, пользуясь приближенной формулой

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 [111] 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208