|
| |
|
Слаботочка Книги Примером совокупности формул с теми же характеристиками точности при меньшем числе обращений к правой части может служить совокупность формул Л-1 = hf{x, у), к2 = / + У + у) А;з = hf (t + , г/ + \{h + к2) . к4 = hf{x + h,y- к2 + 2А;з), к, hf(x + ,y + (7fci + 10А,-2 + , (2) ко = hf (х + ,у + 7(28A;i - 125А;2 + 546кз + 54/4 - 3785) , \ 5 625 / Ау = (fci + 4А,-з + ki) с главным членом погрешности y(x + h) - z{h) =r + 0{h), г = -(42ki + 224/гз + 2U-4 - 162А-5 - 125кв). 336 Если положить y{x(}+h) ~ z{h)+r, то получим метод рассматриваемого типа со значением .s = 5 и соответственно погрешностью на шаге порядка В одной распространенной стандарт1Юй программе управление шагом интегрирования осуществляется по методу, близкому к горизонтальной процедуре из § 3.17. Задаются мерами погрешности на ша-ге ео и £1 < ео и некоторым параметром М > О порядка у. Обычно £i/eo 2 , где / - порядок величины г по h; часто берут ei/eo = 2 . Если ipn{h) = r/max(M, > ео> то шаг признается слишком большим и делается попытка интегрирования, начиная с тех же значений (Хп, Уп), с вдвое более мелким шагом (/г/2). Если (/г) ео, то достигнутая точность признается удовлетворительной. В случае, когда £1 Фnih) ео, следующий шаг берется равным /г, а в случае, когда фп{}г) <£1, -равным 2h. Такой относительно простой способ выбора переменного шага интегрирования часто позволяет решить задачу с существенно меньшими затратами времени ЭВМ по сравнению со случаем интегрирования с постоянным шагом (при той же точности результата). §4. Оценки погрешности одношаговых методов 371 § 4. Оценки погрешности одношаговых методов рассмотрим множество всевозможных методов интегрирования, где последовательно получаются приближения yj к значениям y{xj), хо < xi < .- < XN =хо+Х. Пусть в процессе численного интегрирования к фиксировано и при j к значения yj определяются как значения некоторого функционала Уз = Xj,Xj-k; Уз-\, , Уз-к)- (1) Такой способ численного интегрирования называют к-шаговым. Все построенные выше способы интегрирования имеют следующее общее свойство: приближенное значение решения в следующей точке определялось только в зависимости от значения регпения в предыдущей точке, следовательно, расчетные формулы, соответствующие этим способам, предста-вимы в виде (1) со значением к - 1. Такие методы называются одно-шаговыми. Рассмотрим специальный способ получения оценки погрешности, применимый лишь к одношаговым методам. Запишем формулу (1) в виде %+1 = Ф(/, Xj, Xj+i - Xj ,yj). (2) Получаемые в процессе реальных вычислений приближения к значениям y{xj) связаны не соотношениями (2), а некоторыми соотношениями Уз+1 = Xj, Xj+i - Xj,yj) + Sj+i. (3) Наличие слагаемого Sji обусловлено следующими причинами: 1) округлением чисел при вычислениях; 2) погрешностями в значениях правой части f{x,y); эти погрешности вызваны тем, что рассматриваемая нами функция f{x,y) является некоторым приближением к правой части реального дифференциального Уравнения; кроме того, зачастую в процессе вычисления значений f{x,y) в ЭВМ эта функция приближается другими функциями, что вносит дополнительные погрешности при вычислениях значений правой части; 3) в некоторых случаях значение yj+i определяется из уравнения, эквивалентного (1), но не разрешенного в явном виде относительно переменной yj+i; тогда величина Sj+i содержит составляюшую, являющуюся следствием приближенного решения этого уравнения. Хотя погрешность (5+1 вызвана не только округлением, ее часто называют вычислительной погрешностью на шаге. Точно так же начальное условие уо отличается от значения отыскиваемого решения задачи у{х(}) из-за погрешности в определении исходных данных и округлений. Пусть у(а;)-искомое решение дифференциального уравнения, а ад (ж) - решения, удовлетворяющие условиям yj{xj) = yj (рис. 8.4.1). 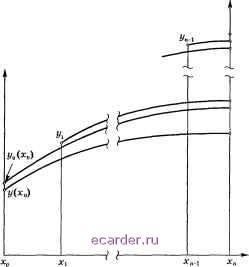 Рис. 8.4.1 Погрешность Rn - Уп{хп) ~ у{хп) можно представить в виде Rn = Уп{Хп) - Уо{Хп) + Уо{Хп) - у{Хп) = (4) = - Уз-Лп)) + (уо(Хп) - У{Хп))- 3 = 1 Разность решений дифференциального уравнения в одной точке может быть выражена через их разность в другой точке следующим путем. Лемма. Пусть Yi (х) и Уг (ж) ~ решения дифференциального уравнени.я у = f{x,y), где f{x,y) - непрерывная и непрерывно дифференцируемая по переменной у функция. Тогда У2(/3) - Ym = (У2(а) - УИа)) ехр /,(ж, у{х)) dx , где у{х) заключено между Y\{x) и Y2{x). Доказательство. Вычтем друг из друга равенства У2 = /(ж,У2), У/-/(ж,Уг). 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 [122] 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 |