|
| |
|
Слаботочка Книги Мы имеем А(() = J\-V {ат/))?) svcr ip, max а((р)= а() = УТ + {аЧ/К огтг \2 Если т = Л/г,2 при т, h О, то шах \X{ip)\ - vl + аЛт = 1 + аАт/2 + 0{т) и условие (4) выполняется; в этом случае следует ожидать устойшвости. Если Иш = оо, то т,/г->0 йо(К1)-0/= и условие (4) не выполняется ни при каком С; тогда сеточная аппроксимация неустойчива. Эта аппроксимация практически не употребляется вследствие более жесткого по сравнению с другими схемами ограничения на шаг т = 0{li), необходимого для устойчивости, и сильного роста (как ещ:){(ГАпт/2}) возмуп],ения решения. Пример 2. Разностная аппроксимация: ft~t-l п п ,п Urn- д> у-1 о (10) Аналогично (9) получаем X{ip) = 1 - ат/h + aT/hexp{-i(p}. Ecjra О < ат/h 1, то (см. рис. 10.2.2) А((р) l-OT/h + OT/h = 1 и следует ожидать устойчивости. Если ат/h = к > 1 при г, /г ~> О, то lim А(7г) = 1 - 2к<-1 и аппроксимация неустойчива вследствие т. Л,->0 СПУ. Аналогично показывается, что следует ожидать устойчивости схемы -Ьа- при а < О и \a\T/h < 1. = 0 (11) изменении в пределах О 27г; стрелка означает направление изменения А((/з) при изменении (/з от О до 27г (при а > 0); на рис. 10.2.1-10.2.4 цифрой 1 обозначен единичный круг. (т,п+1) 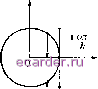 (т-1,п) (т,п) (т+1,п) Рис. 10.2.1    0<Ш-<1 >1 h ~ h Рис. 10.2.2   ах 1 h Рис. 10.2.3    <0  0<<1 п   Рис. 10.2.4 0<<1 О, то lim т, Л,->0 Заметим, что эту аппроксимацию можно рассматривать как (8) с добавленной в нее для устойчивости вязкостью : 2т h? 2т XX Пример 4. Аппроксимация тренога . Приведенные выше аппроксимации имеют первый порядок по совокупности т ш h. Построим аппроксимацию второго порядка; для простоты будем отправляться от аппроксимации (8). Подставляя разложение Тейлора и{х, t) в точке [rnh, пт), имеем {Lh[u]h) = Tunimh, пт)/2 + 0{h) + 0{т). (гп, п) Из дифференциального уравнения (1) получаем ии = aUxx- Приблизим aUxx выражением а{бщ.)т,п- Тогда соответствующая аппроксимация LUf, = О примет вид -;--2h---2---= Так же как и ранее, получаем X{ip) = 1 - i{aT/h)sva.ifi+ {а т/h) {cos ip - 1). Если мы положим X{ip) = x + iy, то (см. рис. 10.2.4) можно написать {х-{1~{ат/к))) у {ат/h) {ат/h) т.е. точки X{ip) лежат на некотором эллипсе в комплексной плоскости, расположенном симметрично относительно оси у = 0. Поскольку Л(7г) = 1 - IctJY? < -1 при \ат/Щ > 1, то в случае \ат/Н\ - const > 1 спектральное условие устойчивости не вьшолнено. Пример 3. Разностная аппроксимация: 2/г 2г /г2 - U, Ц2) . /1 отЛ /1 атЛ ari = (2 - 2fc j + (2 + 2Л j = - Х - При \ат/Н\ 1 имеем (рис. 10.2.3) и следует ожидать устойчивости. Если же \ат/Н\ = к > 1 при т, /i -> л( = \ат1Н\ = к > I и аппроксимация неустойчива. у аппроксимацию можно ] ее для устойчивости вязю /2;-2<+< 1 /г2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 [168] 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 |